Integration by Parts

Integration by Parts

Theorem 1. Let $f$ and $g$ be differentiable functions of $x$. Then 
$$\int f(x) g'(x) dx = f(x) g(x) - \int f'(x) g(x) dx.$$

Proof. By the Product Rule, we have $$\frac{d}{dx} [f(x) \cdot g(x)] = f'(x)g(x) + f(x)g'(x) \\ \Longrightarrow \int \frac{d}{dx} [f(x) \cdot g(x)] = \int f'(x) g(x) dx + \int f(x) g'(x) dx \\ \Longrightarrow \int f(x) g'(x) = f(x) g(x) - \int f'(x) g(x) dx. \blacksquare$$

Integration by Parts for Definite Integrals

Theorem 2. Let $f'$ and $g'$ be continuous over $[a, b]$. Then $$\int_a^b f(x)g'(x) dx = \left[ f(x)g(x) \right]_a^b - \int_a^b f'(x)g(x) dx.$$

Proof. The Fundamental Theorem of Calculus gives the proof. $\blacksquare$

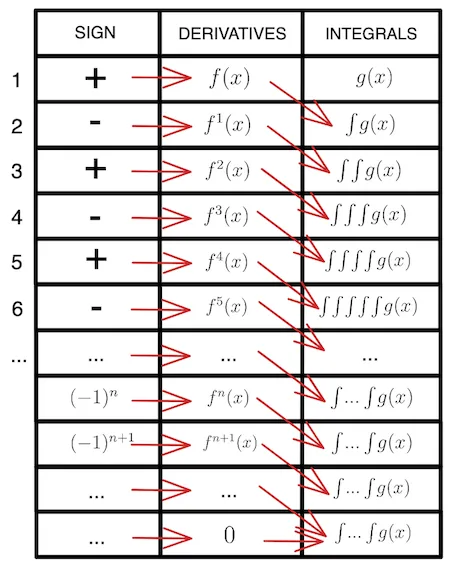
Tabular Integration

Integration by parts(이하 I.B.P), 부분적분을 반복적으로 적용해야 하는 적분의 경우 다소 계산이 귀찮거나 지저분해지는 경우가 생긴다. 이때 tabular integration, 즉 도표적분법이라는 일종의 알고리즘을 적용하면 각각의 적분에 모두 I.B.P를 적용할 필요 없이 한 번에 계산이 가능해진다. 세로 두 줄을 긋고, 왼쪽에는 미분할 함수의 도함수를 나열하고, 오른쪽에는 적분할 함수의 부정적분을 나열한 뒤 왼쪽에서 한 칸 아래 오른쪽으로 이동하여 두 함수를 곱해준다. 이를 차례로 해주는데, 부호는 시작을 +로 하여 한 번씩 -로 교대해 가며 붙여준다. 그리고 부분적분을 더 이상 해줄 필요가 없을 때, 오른쪽에서 같은 줄 왼쪽으로 이동하며 함수를 곱해준 뒤 integral 기호를 붙여주면 된다.

https://arpita95b.medium.com/tabular-integration-faster-accurate-way-to-solve-repeated-integration-by-parts-9cf790239c12