60) 유한 퍼텐셜 우물
앞서 무한 퍼텐셜 우물의 경우를 살펴보았다. 그러나 실제로 입자가 계를 탈출하기 위해 무한한 퍼텐셜 에너지가 필요한 경우는 없으므로, 유한한 퍼텐셜 에너지의 경우를 살펴보는 것이 보다 더 현실적일 것이다.
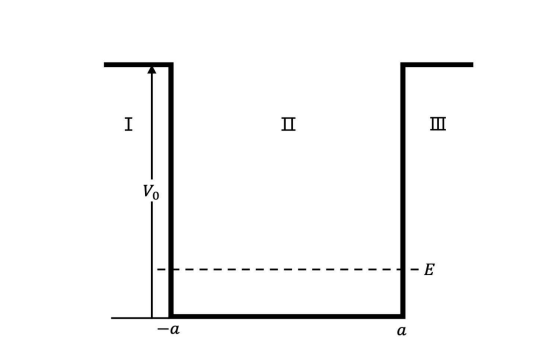
Figure 1과 같이 $x \leq -a \wedge x \geq a$에 해당하는 영역 I, III에서 퍼텐셜은 $V_0$의 값을 가진다. 즉 $V_0$보다 작은 에너지를 가지고 있는 입자는 상자를 벗어날 수 없다. 편의상 이 포스트에서 입자는 항상 $V_0$보다 작은 운동에너지 $E$를 가지고 있다고 가정한다.
무한 퍼텐셜 우물에서는 상자 밖 영역, 즉 I과 III에서 입자를 발견할 확률은 0이었다. 그렇다면 유한 퍼텐셜 우물에서도 그러한지 확인해 보자.
우선 영역 I, III에서 시간 무관 슈뢰딩거 방정식은 다음과 같다.
$$\frac{d^2 \psi}{d x^2} + \frac{2m}{\hbar^2}(E - V_0)\psi = 0$$ 이때
$$\beta = \frac{\sqrt{2m(V_0 - E)}}{\hbar}$$으로 치환하면 방정식은 다음과 같다.
$$\frac{d^2 \psi}{d x^2} - \beta^2 (E - V_0)\psi = 0$$ 이 방정식의 해는 영역 I과 III에서 각각
$$\psi_I = Ce^{\beta x} + De^{-\beta x} \\ \psi_{III} = Fe^{\beta x} + Ge^{-\beta x}$$이다. 이때 $C, D, F, G$는 임의의 상수이다. 이때 각 해가 행실이 좋은 파동함수가 되기 위해서 규격화되어야 하므로 $x \longrightarrow \infty \,\, \text{or} \,\, -\infty$일 때 값이 발산하면 안 된다. 따라서 $D = F = 0$이고,
$$\psi_I = Ce^{\beta x}\\ \psi_{III} =Ge^{-\beta x}$$이다. 이 함수들은 각 영역에서 감소하는 지수함수이다.
영역 II에서는 역시나 자유입자처럼 행동한다고 간주할 수 있고, 무한 퍼텐셜 우물에서 구했던 해를 그대로 가지고 오면
$$\psi_{II} = A\text{sin}kx + B\text{cos}kx$$이다. 이때 $A, B$는 상수이고 $k = \frac{\sqrt{2mE}}{\hbar}$이다. 즉 상자 안에서는 주기함수로 존재한다.
이제 무한 퍼텐셜 우물에서와 같이 경계조건을 적용하자. 역시나 각 경계점에서 파동함수는 연속이고 미분가능해야 한다. 따라서
$$1) \, \psi_I(-a) = \psi_{II}(-a) = -A\text{sin}ka + B\text{cos}ka = Ce^{-\beta a} \\ 2) \, \psi'_I(-a) = \psi'_{II}(-a) = kA\text{cos}ka + kB\text{sin}ka = C\beta e^{-\beta a} \\ 3) \, \psi_{II}(a) = \psi_{III}(a) = A\text{sin}ka + B\text{cos}ka = G e^{-\beta a} \\ 4) \, \psi'_{II}(a) = \psi'_{III}(a) = kA\text{cos}ka - kB\text{sin}ka = -G\beta e^{-\beta a}$$을 만족해야 한다. 이제
$$\xi := ka \wedge \eta := \beta a$$로 치환한 뒤 적당히 경우의 수를 나눠 식들을 연립하자. 컴퓨터를 사용하여 값을 계산하면 양자화된 $\xi_n$을 구할 수 있으며, 따라서
$$E_n = \frac{\hbar^2 k_n^2}{2m} = \frac{\hbar^2 \xi_n^2}{2ma^2}$$을 얻는다.

또한 마찬가지로 파동함수와 그 제곱을 그래프로 표현하면 다음과 같다.
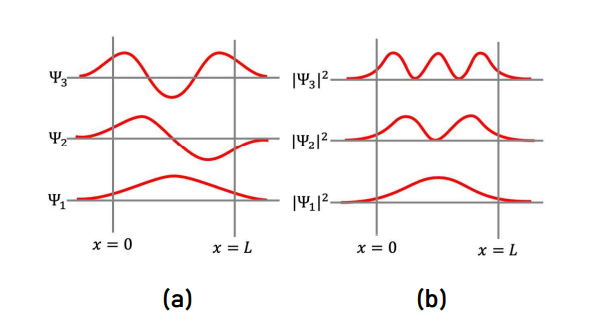
이번에는 무한 퍼텐셜 우물과는 달리 모두 행실이 좋음을 알 수 있다. 앞서 상자 밖의 영역에서는 파동함수가 감소하는 지수함수라고 언급한 바 있다. 따라서 함수의 제곱 역시 유사한 경향성을 가지며, 값이 0보다 큰 영역이 존재한다. 즉 유한 퍼텐셜 우물에서는 상자 밖의 영역에서도 입자가 발견될 확률은 존재하며, 이는 입자의 파동성에 기인한 결과이다.
61) 퍼텐셜 장벽과 양자역학적 터널링
바로 윗문단에서 살펴보았듯이, 유한 퍼텐셜 우물에서는 상자 밖에서도 입자가 존재할 수는 있으나 금세 감소하여 파동함수의 값이 0이 되어버린다.

그러나 Figure 4와 같이 우물 벽의 두께가 적절히 작은 경우 파동함수가 0으로 감소하기 전에 벽을 통과하여 퍼텐셜이 0인 영역으로 나가 다시 자유입자처럼 행동하는 경우를 생각해 볼 수 있다. 고전적으로는 결코 불가능하나, 양자역학적으로 입자는 파동성을 가지므로 벽을 투과할 확률이 존재한다는 것이다. 이러한 현상을 '양자 터널 효과'(Quantum tunnel effect)라고 한다.

Figure 5와 같이 운동 에너지 $E$를 갖는 입자가 높이 $V_0$, 폭 L인 퍼텐셜 우물 벽 왼쪽에서 입사한다고 하자. 벽이 아닌 영역 I, III에서 퍼텐셜은 0이다. 따라서 이 I, III에서 슈뢰딩거 방정식은
$$\frac{d^2 \psi_I}{d x^2} + \frac{2m}{\hbar^2} E\psi_I = 0 \\ \frac{d^2 \psi_{III}}{d x^2} + \frac{2m}{\hbar^2} E\psi_{III} = 0$$이다. 마찬가지로 $k_1 = \frac{\sqrt{2mE}}{\hbar}$로 두면 위 방정식의 해는 각각
$$\psi_I(x) = Ae^{ik_1x} + Be^{-ik_1x} \\ \psi_{III}(x) = Fe^{ik_1x} + Ge^{-ik_1x}$$로 주어진다. 이때 $\psi_I$에서 $Ae^{ik_1x}$은 영역 I에서 오른쪽으로 진행하는 파 $\psi_{I+}$를 의미하며, $Be^{-ik_1x}$는 $\psi_{I+}$이 벽과 충돌한 뒤 부분적으로 반사된 반사파 $\psi_{I-}$를 의미한다.
마찬가지로 $\psi_{III}$에서 $Fe^{ik_1x}$는 영역 $I$에서 투과한 투과파 $\psi_{III+}$를 의미하며, 영역 III에서 왼쪽으로 이동하는 파는 존재하지 않으므로 동일한 논리로 $G = 0$이다.
영역 II에서 슈뢰딩거 방정식은
$$\frac{d^2 \psi_{II}}{d x^2} - \frac{2m}{\hbar^2}(V_0 - E)\psi_{II} = 0$$이고, $k_2 = \frac{\sqrt{2m(V_0 - E)}}{\hbar}$에 대하여
$$\psi_{II}(x) = Ce^{-k_2x} + De^{k_2x}$$의 해를 가진다. 즉 벽 속에서 입자를 발견할 확률이 0이 아니라는 것을 알 수 있다.
동일하게 경계조건을 적용한 뒤, '확률 흐름 밀도'를 도입하여 입자가 우물 벽을 투과할 확률을 구할 수 있다. 두께가 $L$이고 높이가 $V_0$인 퍼텐셜 장벽을 에너지 $E (< V_0)$인 입자가 투과할 확률 $T$는
$$T \simeq e^{-2k_2L}$$로 주어진다. 이때 $L$이 매우 크거나 입자의 에너지 $E$가 매우 작아지면 투과확률은 0에 수렴하는 것을 주목하라. 이는 반대의 경우도 마찬가지며 많은 물리 현상을 설명해 낼 수 있다. 하나씩 설명하면 다음과 같다.
1. $\alpha$ 입자 붕괴: 방사성 핵으로부터 헬륨 원자핵인 $\alpha$ 입자가 탈출하는 현상인 $\alpha$ 붕괴를 양자 터널 현상을 통해 설명할 수 있다. 즉 $\alpha$ 입자는 헬륨 원자라는 퍼텐셜 우물에 갇혀 있고, 이를 투과하는 현상이 $\alpha$ 붕괴이다.
2. 반도체-아디오드 전압-전류 특성: 본래 p-n 접합 다이오드는 불순물을 섞어 넣는 과정인 도핑을 하게 되는데, 적당히 도핑을 할 경우 정전압을 걸어줄 때에 전압에 비례하여 전류가 흐르고, 역전압일 때는 전류가 흐르지 않는 것이 특징이다. 그런데 과하게 도핑을 해줄 경우 터널 현상에 의해 갑자기 전류의 세기가 증가하고 이후 전압에 증가함에 따라 오히려 전류가 감소하는 현상이 나타난다. 이러한 성질을 이용한 다이오드를 '에사키 다이오드'라고 한다.
3. Fowler-Nordheim 전기장 방출: 강한 전기장을 걸어줄 때 금속표면에서 전자가 튀어나오는 현상을 'Fowler-Nordheim 전기장 방출'이라고 한다.

Figure 6과 같은 상황에서, 본래 외부 자기장이 존재하지 않을 때는 금속 안에 있는 전자들에 대해서 퍼텐셜 장벽의 두께 $L$이 매우 커서 투과 확률이 0에 가깝다. 그러나 외부 자기장을 걸어줄 경우 퍼텐셜 장벽은 전기장의 세기 $E$에 대해 $V = -eEx$로 주어지며, 이는 기울기가 $-eE$인 직선이다. 따라서 Figure 6 (b)와 같이 $L$이 충분히 작아져서 터널 현상이 일어날 수 있으며, 전자가 방출되는 것을 확인할 수 있다.
4. 주사 터널 현미경(STM; Scanning Tunneling Microsope): 시료의 미세한 표면구조를 살펴보거나 물질을 구성하는 원자를 들여다볼 수 있는 장치를 주사 터널 현미경, STM이라고 부른다.

장치는 Figure 7과 같이 구성되어 있다. 전압을 걸어주어서 탐침과 샘플 표면 사이에 전기장을 형성해 준다. 이때 터널 현상으로 탐침에서 샘플 표면으로 전류가 흐르게 된다. 샘플 표면을 $x-y$ 평면으로 둘 때 탐침이 이 평면을 스캔하게 되고, 탐침과 시료 표면 사이의 거리에 따라 퍼텐셜 장벽의 두께 $L$이 변하게 되므로 각 위치에 따라 순간적으로 전류의 세기가 달라지게 된다. 이때 이렇게 바뀌는 전류값을 영상으로 변환하면 Figure 7 (b)와 같이 물질을 구성하는 원자의 모습을 확인할 수 있다. 이 사진은 $Si$의 표면 STM 사진이다.