Green's Theorem
Theorem 1. Let $C$ be a piecewise smooth, simple closed curve enclosing a region $R$ in the plane. Let $\mathbf{F}(x, y) = \langle M(x, y), N(x, y) \rangle$ be a vector field with $M$ and $N$ having continuous first partial derivatives in an open region containing $R$. Then the counterclockwise circulation of $\mathbf{F}$ around $C$ equals the double integral of $(\nabla \times \mathbf{F}) \cdot \mathbf{k}$ over $R$. $$\oint_C \mathbf{F} \cdot d \mathbf{r} = \iint_R \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) dA$$
Theorem 2. Let $C$ be a piecewise smooth, simple closed curve enclosing a region $R$ in the plane. Let $\mathbf{F}(x, y) = \langle M(x, y), N(x, y) \rangle$ be a vector field with $M$ and $N$ having continuous first partial derivatives in an open region containing $R$. Then the outward flux of $\mathbf{F}$ across $C$ equals the double integral of $\nabla \cdot \mathbf{F}$ over $R$ enclosed by $C$. $$\oint_C \mathbf{F} \cdot \mathbf{n} ds = \iint_R \left( \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} \right) dA$$
Green's Theorem은 위와 같이 두 개의 형태가 있으며, 각각 circulation-curl, flux-divergence로 대응된다. 두 정리는 벡터장 $\mathbf{F}$를 변형해주면 각각 성립하므로 서로 동치이다.
직관적인 이해는 다음과 같다. 평면 영역 $R$이 있을 때, $R$ 전체에 대해서 어떤 유체와 같은 대상이 얼마나 회전하고 있는지를 파악하고자 한다. 원칙적으로는 $R$의 모든 $dA$에 대해서 curl을 적분해야 한다. 그러나 $R$을 $x, y$축으로 잘게 쪼개고 각 piece에 대해서 curl을 생각하면 인접한 piece들이 맞닿아 있는 부분은 크기는 같고 방향은 반대인 회전 성분을 가지므로 서로 상쇄됨을 직관적으로 알 수 있다. 이런 식으로 계산하다보면 결국 영역 전체의 curl은 $R$의 테두리만 고려하면 됨을 알 수 있고, 이는 circulation이다. Flux 형태도 마찬가지로 생각할 수 있다.
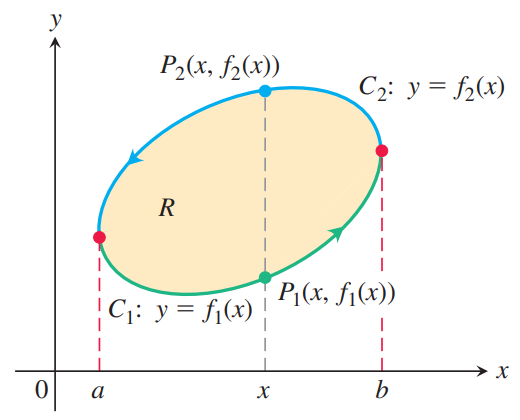
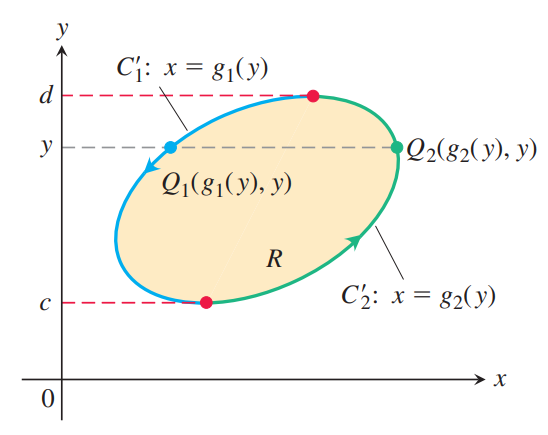
Proof of Theorem 1. The curve $C$ can be expressed by two different curves: $$C_1: y = f_1(x), a \leq x \leq b, \quad C_2: y = f_2(x), b \geq x \geq a.$$ Then we have $$\iint_R \frac{\partial M}{\partial y} dy dx = \int_a^b \int_{f_1(x)}^{f_2(x)} \frac{\partial M}{\partial y} dy dx = \int_a^b (M(x, f_2(x)) - M(x, f_1(x))) dx \\ = - \int_b^a M(x, f_2(x)) dx - \int_a^b M(x, f_1(x)) dx = - \int_{C_2} M dx - \int_{C_1} M dx = - \oint_C M dx.$$ Similarly, we can integrate $\frac{\partial N}{\partial x}$ on the region $R$. We can divide $C$ by two distinct curves $C'_1$ and $C'_2$: $$C'_1: x = g_1(y), d \geq y \geq c, \quad C'_2: x = g_2(y), c \leq y \leq d$$ Then we obtain $$\iint_R \frac{\partial N}{\partial x} dx dy = \int_c^d \int_{g_1(y)}^{g_2(y)} \frac{\partial N}{\partial x} dx dy = \int_c^d (N(g_2(y), y) - M(g_1(y), y)) dy \\ = \int_c^d N(g_2(y), y) dy + \int_d^c N(g_1(y), y) dx = \int_{C'_2} N dy + \int_{C'_1} N dy = \oint_C N dy.$$ Summing these two equations gives $$\oint_C N dy - M dx = \iint_R \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) dA. \blacksquare$$