Cylindrical Coordinates
Definition 1. Cylindrical coordinates represent a point $P$ in space by ordered triples $(\rho, \phi, z)$ in which $r \geq 0$.
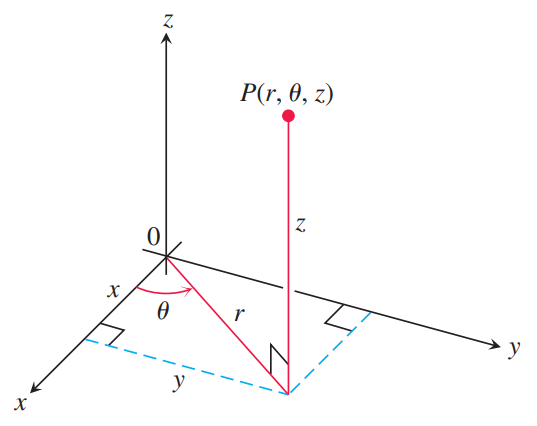
단순히 polar coordinates에다가 $z$ 성분만 추가한 3차원 좌표계이다. 위 그림에는 $(r, \theta, z)$로 나타냈지만 생새우초밥집 저자의 주장을 받아들여 $(\rho, \phi, z)$로 쓰도록 하자.
원통 좌표계는 좌표공간에서 cartesian coordinates과 자유롭게 변환할 수 있다. $(x, y, z)$는 $(\rho \cos \phi, \rho \sin \phi, z)$로 바꿀 수 있으며, 반대로 $(\rho, \phi, z)$는 $(\sqrt{x^2 + y^2}, \tan^{-1}(\frac{y}{x}), z)$로 바꿀 수 있다. $z$는 동일하고, polar coordinates에서 했던 변환을 반복한 것이나 다름없다.
$x = \rho \cos \phi, y = \rho \sin \phi, z = z$라는 변환에 대해서 Jacobian을 구하면 $$\begin{vmatrix} \frac{\partial x}{\partial \rho} & \frac{\partial x}{\partial \phi} & \frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial \rho} & \frac{\partial y}{\partial \phi} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial \rho} & \frac{\partial z}{\partial \phi} & \frac{\partial z}{\partial z} \end{vmatrix} = \begin{vmatrix} \cos \phi & - \rho \sin \phi & 0 \\ \sin \phi & \rho \cos \phi & 0 \\ 0 & 0 & 1 \end{vmatrix} = r$$이므로 polar coordinates와 동일하다.