Stokes's Theorem

Stokes's Theorem 

Theorem 1. Let $S$ be a piecewise smooth oriented surface having a piecewise smooth boundary curve $C$. Let $\mathbf{F} = \langle M, N, P \rangle$ be a vector field whose components have continuous first partial derivatives on an open region containing $S$. Then the circulation of $\mathbf{F}$ around $\mathbf{C}$ in the direction counterclockwise with respect to the surface’s unit normal vector $\mathbf{n}$ equals the integral of the curl vector field $\nabla \times \mathbf{F}$ over $S$: $$\oint_C \mathbf{F} \cdot d \mathbf{r} = \iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} d \sigma \\ = \iint_S (\nabla \times \mathbf{F}) \cdot d \mathbf{a}.$$

스토크스 정리는 그린 정리의 첫번째 버전을 3차원으로 확장시킨 버전이다. 위 정리에서 $R$은 $xy$ 평면 위에 있는 plane이며 $C$에 의해 둘러싸여 있다고 할 때, $d \sigma = dx dy$이고 $\mathbf{n} = \mathbf{k}$이므로 $$(\nabla \times \mathbf{F}) \cdot \mathbf{n} = (\nabla \times \mathbf{F}) \cdot \mathbf{k} = \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right)$$ 이다. 따라서 스토크스 정리는 그린 정리를 함의한다.

 

정리에서 $S$는 piecewise smooth surface으로, smooth surface를 여러 개 이어붙인 surface를 말한다. 스토크스 정리는 boundary curve $C$가 동일하다면 곡면 $S$의 모양과는 무관하게 flux의 값이 같다고 말한다. 즉 위 적분의 값은 오직 curve $C$에 의존하는 것이다. 이는 보존장의 선적분이 구간 양 끝점에만 의존한다는 path independence의 성질과 유사하다. 즉 곡면 내부의 정보는 오로지 경계면에 의해서만 결정된다고 요약할 수 있다. 

Proof. We assume that the equation of $S$ is $z = g(x, y), (x, y) \in D$, where $g$ has continuous second partial derivatives and $D$ is a simple plane region whose boundary curve $C_1$ corresponds to $C$. Let's consider the level surface $F(x, y, z) = z - g(x, y) = 0$, and the normal vector field $\mathbf{n}$ of $F$ is $\mathbf{n} = \nabla F = \langle - \partial_x g, - \partial_y g, 1 \rangle$. Thus we have $$\iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} d \sigma \\ = \iint_S \left[ - \left( \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z} \right) \frac{\partial g}{\partial x} - \left( \frac{\partial M}{\partial z} - \frac{\partial P}{\partial x} \right) \frac{\partial g}{\partial x} + \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) \right] d\sigma .$$ If $x = x(t), y = y(t), a \leq t \leq b$ is a parametric equation of $C_1$, then a parametric representation of $C$ is $x = x(t), y = y(t), z = g(x(t), y(t)), a \leq t \leq b$. This allows us to evaluate the line integral as follows: $$\oint_C \mathbf{F} \cdot d \mathbf{r} = \int_a^b \left( M \frac{dx}{dt} + N \frac{dy}{dt} + P \frac{dg}{dt} \right) dt \\ = \int_a^b \left[ M \frac{dx}{dt} + N \frac{dy}{dt} + P \left( \frac{\partial g}{\partial x} \frac{dx}{dt} + \frac{\partial g}{\partial y} \frac{dy}{dt} \right) \right] dt \\ = \int_a^b \left[ \left( M + P \frac{\partial g}{\partial x} \right) \frac{dx}{dt} + \left( N + P \frac{\partial g}{\partial y} \right) \frac{dy}{dt} \right] dt \\ = \int_{C_1} \left( M + P \frac{\partial g}{\partial x} \right) dx + \left( N + P \frac{\partial g}{\partial y} \right) dy \\ = \iint_S \left[ \frac{\partial}{\partial x}\left( N + P \frac{\partial g}{\partial y} \right) - \frac{\partial}{\partial y} \left( M + P \frac{\partial g}{\partial x} \right) \right] d\sigma$$ where we have used Green's Theorem in the last step. Then, using the chain rule to $M, N$ and $P$, we get $$\oint_C \mathbf{F} \cdot d \mathbf{r} =  \iint_S \left[ - \left( \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z} \right) \frac{\partial g}{\partial x} - \left( \frac{\partial M}{\partial z} - \frac{\partial P}{\partial x} \right) \frac{\partial g}{\partial y} + \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) \right] d\sigma \\ = \iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} d \sigma. \blacksquare$$

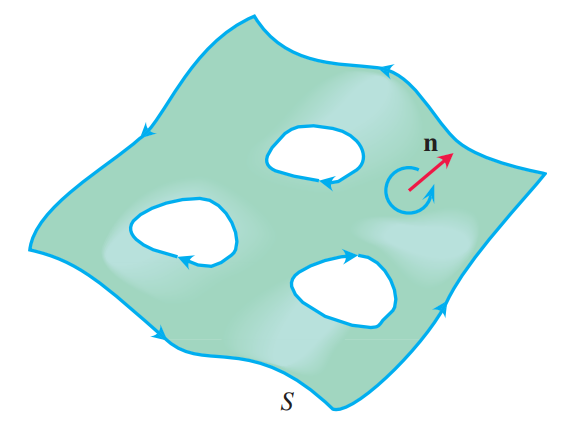
스토크스 정리는 곡면 $S$가 다음 그림과 같이 유한 개의 구멍이 있어도 여전히 성립한다. 이때 경계면은 구멍의 경계면까지 포함해야 하며, $S$의 바깥 경계면이 counterclockwise일 때 방향은 clockwise로 잡는다. 즉 경계면을 따라 걸었을 때 왼쪽에 내부면이 위치하도록 잡는 것이다. 

Thomas Calculus 14e 995p.