34) 흑체 복사와 레일리 - 진스 공식
양자역학이 어떻게 학문으로써 대두될 수 있었는지에 대해 그 역사적 배경을 알아보고자 한다. 양자역학의 태동은 18세기에서 19세기, 산업혁명과 강대국들의 식민지 확장에 따른 제철산업의 발달로부터 일어났다. 국가의 과학기술의 발달은 곧 그 국가가 가지는 경쟁력과 비례하곤 한다. 자연스럽게 당시 유럽의 과학계 또한 국가적 사업을 뒷받침하기 위한 이론적 배경을 만드는 것에 집중되어 있었고, 따라서 열물리학이나 분광학과 같은 학문이 발전하게 되었다. '흑체 복사'(Black Body Radiation)에 관한 연구 또한 그 일련의 연구 중 하나였는데, '흑체'(Black Body)란 진동수와 입사 관계없이 모든 전자기파를 100% 흡수하는 이상적인 물체이다.

위 그림과 같이 '공동'(Cavity)이라는 구형태의 물체를 고려하자. 빛알갱이, 즉 하나의 광자가 한 번 들어가면 다시 나오지 않을 정도로 작은 구멍이 있을 때 이 구멍으로 빛을 입사시켰다고 해보자. 이때 흡수와 방출을 반복하여 끝내 빛이 100% 흡수된다면, 다시 말해 빛이 다시 바깥으로 빠져나오지 않는다면 공동은 흑체로 간주할 수 있다.
흑체는 전자기파를 완전히 흡수하여 열평형 상태에 도달한다면 위에서 언급한 '흑체 복사'라는 복사선을 방출하게 된다. 이 흑체 복사의 파장에 따른 세기를 그래프로 그리면 아래 그림에서 빨간색 곡선과 같이 나타난다.
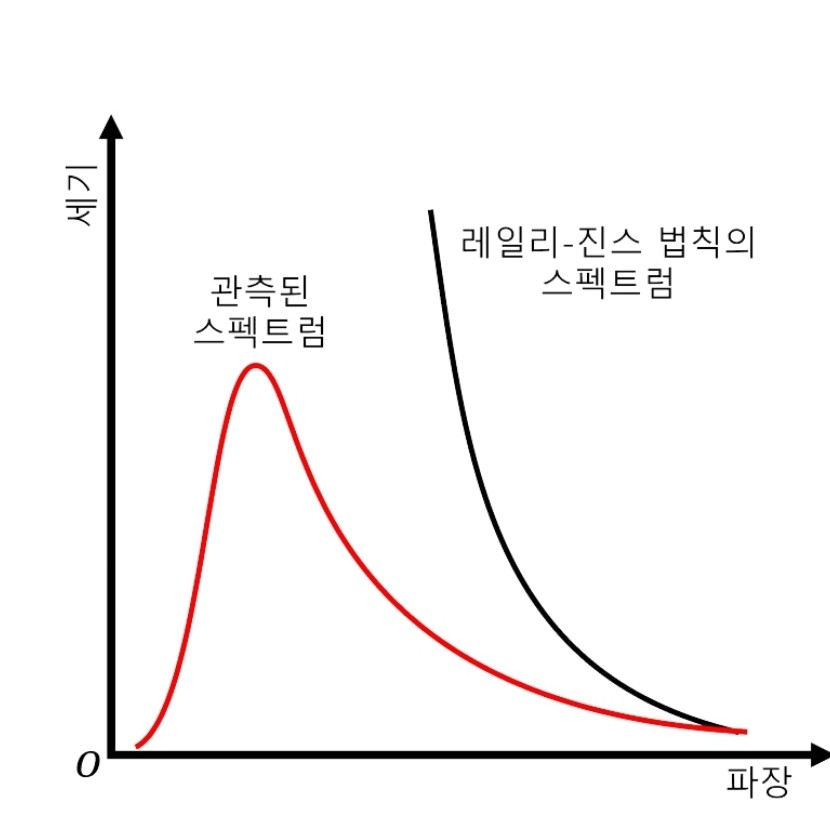
1900년 물리학자 레일리(L. Rayleigh)와 진스(J. Jeans)는 이 곡선을 나타내는 공식을 찾아내어 '레일리 - 진스 공식'을 발표하게 된다. 흑체가 빛과 같은 전자기파를 흡수하면 흑체를 구성하는 분자들이 열, 즉 에너지를 얻어 진동운동을 하고, 복사파를 방출할 것이다. 레일리와 진스는 공동이 완전 반사체로 이루어져 있다고 가정하고, 이 복사파는 진폭이나 파장, 주기의 변화 없이 공동 내부에서 끊임없이 방출되어 반사될 것이므로 진동자가 만들어내는 진행파와, 이와 진행 방향이 반대인 반사파가 중첩하여 정상파를 만들어야 한다고 생각했다. 또한 이 정상파 조건으로부터 진동수가 $\nu \sim \nu + d \nu$ 사이에 있는, 공동 속에 있는 단위 부피당 정상파의 개수 $G(\nu)d \nu$ 는
$$G(\nu)d \nu = \frac{8 \pi \nu ^2 d \nu}{c^3}$$임이 됨을 알아냈다. 이때 $c$는 광속이다.
흑체가 절대온도 T에서 열평형을 이루고 있을 때 정상파는 개당
$$\bar{\epsilon} = k_B T$$의 평균 에너지 밀도를 가진다. 이때 $k_B$는 볼츠만 상수이다. 고전적인 관점에서 진동자의 총 에너지 $E$는 운동 에너지와 퍼텐셜 에너지의 합으로 작성할 수 있고, 에너지 등분배 정리에 따라 각 에너지에는
$$\frac{1}{2}k_B T$$의 평균 에너지가 할당된다. 따라서 $\nu \sim \nu + d \nu$의 진동수 범위에서 공동 내 단위 부피당 에너지 $u(\nu)d \nu$ 는 (개당 정상파 평균 에너지) * (단위 부피당 정상파 개수)이므로
$$u(\nu)d \nu = \bar{\epsilon} G(\nu)d \nu = \frac{8 \pi k_B T}{c^3} \nu ^2 d \nu$$이 성립하고, 이것이 바로 레일리와 진스가 찾아낸 공식이다. 즉 에너지는 진동수의 제곱에 비례하게 되고, 따라서 파장에 따른 흑체 복사의 세기를 그래프로 그리면 자외선과 같은 낮은 파장대에서는 아주 큰 세기를 가지게 된다. 그러나 이러한 이론적 결과는 실제 관측된 값과는 현격히 다른 분포를 보였고, 특히 자외선 영역에서는 그 정도가 심하여 이 영역에서의 판이한 불일치를 '자외선 파탄'(Ultraviolet Catastrophe)라 부른다.
당시 많은 물리학자들은 이러한 이론과 실험의 불일치는 레일리 - 진스 공식의 유도 과정에 원인이 있다고 보았지만, 문제가 되는 부분을 찾을 수 없었다. 막스 플랑크(Max Planck) 역시 이 문제를 해결하려 노력했던 사람 중 한 명이었으며, 플랑크가 이 문제를 해결하기 위해 Ad Hoc Hypothesis를 사용하면서부터 본격적인 양자론이 시작되었다고 볼 수 있다.
35) 플랑크의 양자 가설
플랑크는 레일리 - 진스 공식의 유도과정에서 문제를 찾을 수 없자 여러 시도 끝에 관측된 흑체 복사 곡선에 딱 들어맞는 공식을 짜 맞추게 된다. 1900년, 플랑크가 새로 도입한 에너지 밀도 공식은 다음과 같다.
$$u(\nu)d \nu = \frac{8 \pi h}{c^3} \frac{\nu ^3 d \nu}{e^{\frac{h \nu}{k_B T}} - 1}$$
여기서 플랑크는 '플랑크 상수'라 하는 상수 $h$를 도입했고, $h$가
$$h = 6.626 \cdot 10^{-34} J \cdot s$$의 값을 가질 때 관측된 곡선과 가장 잘 들어맞게 된다. 위 식에서 $e$의 지수 부분을 주목하자. 분모에 해당하는 $k_B T$는 앞서 보았듯이 에너지의 차원을 가지므로, 분자에 해당하는 $h \nu$ 또한 에너지의 차원을 가져야 함은 자명하다.
고전적인 물리학의 관점에서 에너지는 분명히 연속적인 물리량이다. 위에서 살펴본 레일리 - 진스 공식의 유도 과정에서 진동자의 운동 에너지는 개당 정상파의 평균 에너지 값의 절반과 같다. 운동 에너지는 진동자의 속도의 크기 제곱에 비례하게 되고, 속도는 연속적으로 변화하므로 정상파의 에너지 또한 연속적으로 바뀐다. 플랑크는 여기서 에너지가 연속적으로 변한다는 고전적인 관점을 버리고, 에너지는 불연속적인 물리량이라는 길을 택한다. 즉 에너지 밀도는 동일하지만 개당 정상파가 가지는 에너지가 연속적이지 않고 불연속적이라는 것이다.

플랑크에 의하면, 위의 그림과 같이 진동자의 에너지 $E_n$은 불연속적이며,
$$E_n = nh \nu (n = 0, 1, 2, ...)$$의 값을 가진다. 따라서 진동자는 $h \nu$를 최소 단위로 하여 에너지를 흡수 또는 방출하게 되며, 임의의 에너지 상태 $n$과 $n-1$ 혹은 $n$과 $n+1$ 사이의 에너지 값은 가질 수 없다. 플랑크는 최소 에너지 단위인 $h \nu$를 가지는 에너지 알갱이를 '양자'(Quantum)라고 부르며, 진동자의 에너지가 '양자화'(Quantization)되어 있다고 하였다. 이와 같이 에너지는 연속적인 물리량이라는 고전적인 관념을 버리고 불연속적인 에너지의 개념을 도입한 플랑크의 가설을 '양자가설'(Quantum Hypothesis)이라고 부른다.
플랑크의 에너지 밀도 공식에서 $h \nu$ >> $k_B T$의 경우, 즉 높은 진동수를 가진다면 에너지 밀도 $u(\nu)d \nu$는 0으로 수렴한다. 따라서 레일리 - 진스 공식에서 문제가 되었던 자외선 파탄의 문제가 해결된다. 또한 $h \nu$ << $k_B T$의 경우, 즉 낮은 진동수에서는
$$\frac{1}{e^{\frac{h \nu}{k_B T}} - 1} \simeq \frac{1}{1 + \frac{h \nu}{k_B T} - 1} = \frac{k_B T}{h \nu}$$로 근사되므로, 에너지 밀도 $u(\nu)d \nu$는 다음과 같이 레일리 - 진스 공식으로 환원되며 정상파의 개당 평균 에너지는
$$u(\nu)d \nu = \frac{8 \pi h}{c^3} \frac{\nu ^3 d \nu}{e^{\frac{h \nu}{k_B T}} - 1} \simeq \frac{8 \pi k_B T}{c^3} \nu ^2 d \nu = \bar{\epsilon} G(\nu)d \nu \\ \Longrightarrow \bar{\epsilon} = \frac{h \nu}{e^{\frac{h \nu}{k_B T}} - 1}$$로 계산된다. 즉 온도 $T$뿐만 아니라 복사파의 진동수에도 의존한다.
이러한 플랑크의 양자가설은 결과적으로 실험 결과를 잘 설명해주긴 했지만, 본질적으로 그 유도 과정은 완전하지 못했다. 플랑크는 고전 물리학의 관점을 포기하고 새로운 관점을 제시함으로써 양자론의 시대를 열었지만, 정작 그 자신은 이후의 양자 개념에 대해서는 보수적인 태도를 견지했다고 한다. 이후 양자가설이 발표되고 5년 뒤인, 기적의 해 1905년에 아인슈타인이 광전효과에 대한 새로운 해석을 내놓음으로써 본격적인 양자역학이 시작되었다고 볼 수 있다.