Simply Connected Region
Definition 1. Let $D$ be an open region.
(1) $D$ is connected if any two points in $D$ can be joined by a smooth curve that lies in the region.
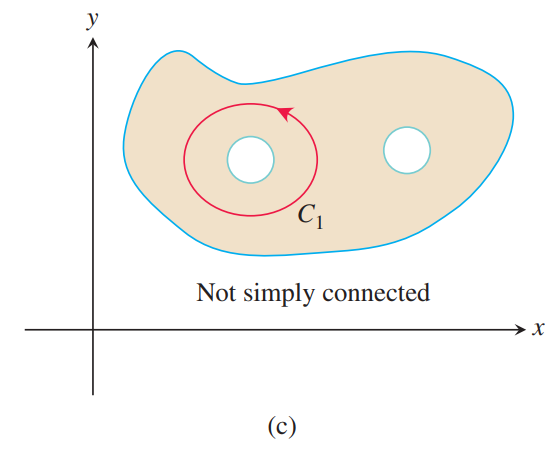
(2) $D$ is simply connected if every loop in $D$ can be contracted to a point in $D$ without every leaving $D$.
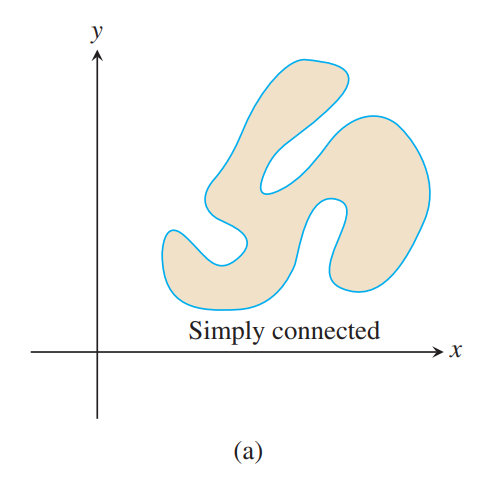
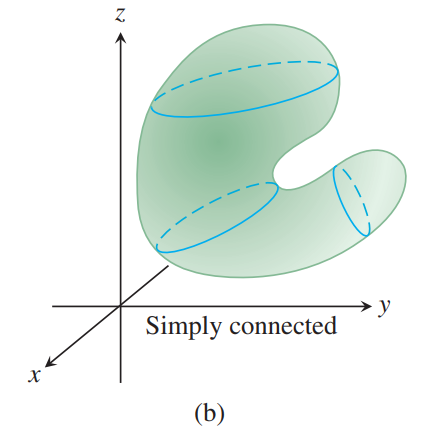

말 그대로, 영역 $D$ 안에 임의의 두 점이 그 영역 안에 포함된 곡선에 의해 연결될 수 있다면 $D$는 connected region이다. 만약 $D$가 겹치치 않는 두 disk이고 각 disk에서 한 점씩 뽑아보자. 그러면 두 점을 연결하면서 영역 $D$안에 포함되는 곡선은 존재하지 않으므로 이 경우 $D$는 connected가 아니다.
Simply connected region은 connected region이면서 어떤 hole도 없는 경우를 말한다. 위 그림의 (c), (d)는 hole을 포함하고 있으므로 $D$에 있으면서 한 점으로 수축될 수 없는 loop가 존재하므로 simply connected가 아니다.
보다 더 수학적으로 엄밀한 정의는 미분기하학 교재를 살펴보자.