1897년, 톰슨(J. J. Thomson)은 음극선 실험을 통해 전자의 존재를 규명했다. 교과서에서 음극선 실험을 소개할 때 주로 톰슨의 이름만 등장하는 것과는 달리, 음극선 실험은 대략 50년 전부터 이미 그 연구가 활발히 진행되었었다. 다만 결정적으로 음극선이 '전자'라는 아원자임을 밝혀낸 것은 톰슨이기에 주로 그가 수행한 음극선 실험이 많은 이들에게 알려져 있다. 톰슨은 전자가 음의 전하를 띠는 입자임을 밝혀냈지만, 그 전하량과 질량을 각각 밝혀내진 못했다. 그러나 전하량과 질량의 비인 '비전하'값 $\frac{e}{m}$을 알아냈는데, 이 포스트에서는 톰슨이 비전하를 측정한 과정을 소개하고자 한다.
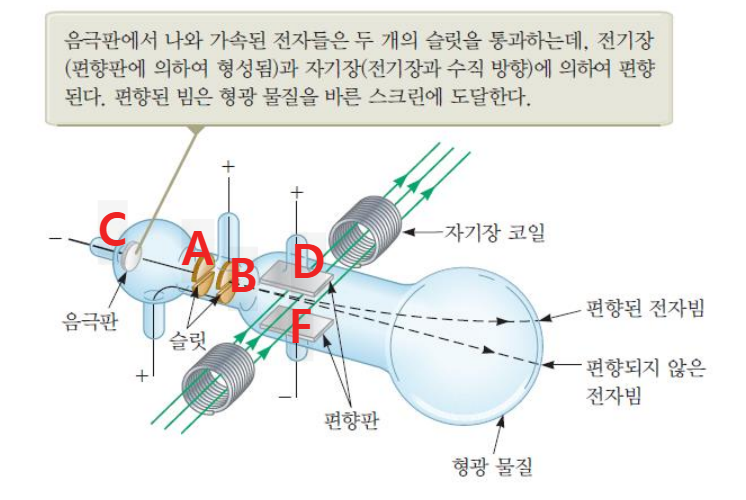
실험 기구는 Figure 1과 같다. 왼쪽부터 음극판 C와 음극선이 통과할 수 있는 두 개의 슬릿 A, B, 그리고 음극선을 편향시키는 편향판 D, F와 자기장 코일이 있고, 끝에는 음극선이 닿아서 발광하게 만드는 형광 물질이 칠해져 있다.
기본적으로 유리관은 진공 상태에 있다. 우선 전극 사이에 전압을 인가하면 음극판 C에서 음극선이 방출되어 A로 향한다. B는 A와 동일한 전위를 가지는데, 슬릿의 크기가 더 작아서 이동하는 음극선, 즉 전자의 양을 조절한다. Figure 1에서 알 수 있듯 A와 B는 접지되어 C에 대해 상대적으로 양극을 가진다. 음극선은 B를 통과해 편향판 D, F를 지나 끝부분에 도달해 발광점을 만든다. 이때 D와 F는 전원에 연결되어서 전기장을 형성하고, 음극선은 전기장의 반대 방향으로 편향된다.
한편 코일에 전류를 흘려서 전기장에 수직이 되도록 자기장을 걸어준다. 이때 전기력과 자기력의 방향은 반대이므로 음극선이 편향되지 않고 수평으로 나아갈 수 있도록 각각 크기를 조절해 줄 수 있다. 즉
$$eE = ev_x B \\ \Longrightarrow v_x = \frac{E}{B}$$이다. 이때 $e$는 전자의 전하량, $E$와 $B$는 각각 전기장, 자기장의 세기, $v_x$는 전자의 수평방향 속도의 크기이다. 편의를 위해 Figure 2와 같이 나타내자.

자기장을 제거하고 전기장만 걸려져 있는 상황을 고려하자. 이때 전자는 전기력 만을 받으므로 수직방향으로 편향된다. 편향판을 통과하기 전 전자의 속력은 위에서 구한 $v_x$와 같고, 전자가 편향판의 길이 $x_1$을 통과하는 데 걸린 시간 $t_1$은
$$t_1 = \frac{x_1}{v_x}$$이다. 또한 전기장에 의해 수직 방향으로 가속되므로 가속도 $a$는
$$ma = eE \\ \Longrightarrow a = \frac{eE}{m}$$이다. 이때 $m$은 전자의 질량이다.
따라서 수직 방향 이동거리 $y_1$은 등가속도 운동 공식에 의해
$$y_1 = \frac{1}{2}a t^2_1 = \frac{1}{2} (\frac{eE}{m}) (\frac{x_1}{v_x})^2$$이다.
편향판을 지나고 나면 전자는 등속도 운동을 한다. 따라서
$$x_2 = v_x t_2 \\ \Longrightarrow t_2 = \frac{x_2}{v_x}$$이며, 기구 끝에 닿기 전까지 이동한 수직거리 $y_2$는 $y_2 = v_y t_2$로 주어진다. $v_y$는 편향판에서 가속된 속도로 $v_y = at_1$이다. 즉
$$y_2 = at_1 (\frac{x_2}{v_x}) = \frac{eE}{m} (\frac{x_1}{v_x}) (\frac{x_2}{v_x}) = \frac{eE}{m} \frac{x_1x_2}{v^2_x}$$이다.
따라서 총 편향된 거리 $y = y_1 + y_2$는
$$y = y_1 + y_2 = \frac{1}{2} (\frac{eE}{m}) (\frac{x_1}{v_x})^2 + \frac{eE}{m} \frac{x_1x_2}{v^2_x} \\ = \frac{eE}{m} \frac{x_1}{v^2_x} (\frac{1}{2} x_1 + x_2) = \frac{eE}{m} x_1 (\frac{B}{E})^2 (\frac{1}{2} x_1 + x_2) = \frac{e}{m} (\frac{B^2}{E}) x_1 (\frac{1}{2} x_1 + x_2) \\ \Longrightarrow \frac{e}{m} = \frac{2yE}{B^2 x_1 (x_1 + 2x_2)}$$이다. 이때 $y, B, E, x_1, x_2$ 등은 측정 및 조절 가능한 값들이므로 비전하 $\frac{e}{m}$을 구할 수 있고, 그 값은 약
$$\frac{e}{m} = 1.758802 \cdot 10^{11} C \cdot kg^{-1}$$이다. 톰슨은 이 실험에서 평균적으로 $$\frac{e}{m} = 0.7 \cdot 10^{11} C \cdot kg^{-1}$$을 얻었다고 한다. 실제 값과는 약간 차이가 있으나, 당시의 장비로서는 상당히 정확했다고 볼 수 있다.
톰슨의 방법과는 약간 다른, 질량 분석계(Mass spectrometer)를 통해서 조금 더 간단하게 비전하값을 구할 수 있다.
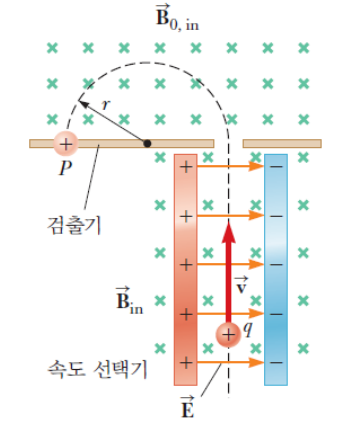
질량 분석계는 원자와 분자 이온들을 질량 대 전하 비율에 따라 분리시키는 장치이다. Figure 1과 같은 그림의 장치는 베인브리지 질량 분석계(Bainbridge mass spectrometer)이다. 분석계는 전기장과 자기장이 모두 작용하는 구간과 자기장만 작용하는 구간으로 나뉜다. 첫번째 구간의 경우, 톰슨의 실험에서도 보았듯이 편향되지 않는 속도를 가진 입자만 통과된다.1 이후 두번째 구간에서는 자기력만 받으므로 등속 원운동을 하여 검출기의 한 점에 부딪히게 된다. 두번째 구간에서 편향되는 방향은 입자의 부호에 따라 다르다.
음극선의 경우를 생각해보자. 첫번째 구간에서의 전자의 속도 $v$는 $$v = \frac{E}{B_1}$$로 주어진다. 이때 $E$는 전기장의 세기, $B_1$는 첫번째 구간의 자기장의 세기이다. 두번째 구간에서 전자는 등속 원운동하므로 $$evB_2 = m\frac{v^2}{r} \\ \Longrightarrow \frac{e}{m} = \frac{v}{B_2r} = \frac{E}{B_1 B_2 r}$$이다. 이때 $B_2$는 두번째 구간의 자기장의 세기이다. 마찬가지로 $E, B_1, B_2, r$은 측정 및 조절 가능한 값이므로 비전하값을 알 수 있다.
- 이를 속도 선택기(Velocity Selector)라고 부른다. [본문으로]