40) 분광학자들의 궁금증

1900년도 초기의 분광학자들에게는 당시 이론으로는 설명할 수 없는 현상 하나가 있었다. 태양광이나 흑체에서 나오는 빛을 분광기를 통해 스펙트럼으로 나타내면 Figure 1의 첫 번째 스펙트럼과 같이 연속 스펙트럼을 얻는다. 즉 파장이 연속적으로 분포해 있다는 것이다. (태양 내부나 표면의 가스에 의해 일부 파장이 흡수되긴 하지만, 대부분 연속적인 파장을 갖는다.)그러나 진공 방전관에 수소 원자를 넣어서 얻은 빛을 스펙트럼으로 나타내면 두 번째 스펙트럼과 같이 불연속적인 선 스펙트럼을 얻고, 이 흡수선들의 분포에는 일정한 규칙이 존재했다.
1885년, 발머(J. Balmer)는 수소 원자 스펙트럼의 가시광선 영역에서 나타난 4개의 방출선(410.1nm, 434.0nm, 486.1nm, 656.3nm)을 찾았고, 스펙트럼의 파장값 $\lambda$를 예측하는 공식을 만들었다.
$\lambda = B(\frac{n^2}{n^2 - 2^2}) (n = 3, 4, ...)$ 여기서 $B = 356.56nm$의 상수다.
뒤이어 1888년, 리드버그(J. Rydberg)는 조금 더 실험값에 근접한 발머의 공식을 일반화한 공식을 만들었다.
$$\frac{1}{\lambda} = R_H (\frac{1}{m^2} - \frac{1}{n^2}) (m = 2, n = 3, 4, ...)$$ 여기서 $R_H = 1.09737 \cdot 10^7 m^{-1}$의 상수로, '리드버그 상수'라 부른다. 이때 $m = 2$는 가시광선 영역에서의 파장값을 얻기 위해 둔 값이다.
이어서 1906년 라이먼이 자외선 영역에서($m = 1, n = 2, 3, ...$), 1908년 파센($m = 3, n = 4, 5, ...$), 1922년 브래킷($m = 4, n = 5, 6, ...$), 1924년 푼트($m = 5, n = 6, 7, ...$)가 적외선 영역에서 차례로 수소 원자의 선 스펙트럼의 계열을 찾아냈고 이 값들은 리드버그의 공식으로 잘 예측이 가능했다.
이처럼 실험결과에 들어맞는 공식을 짜맞추기 까지는 가능했으나, 구체적으로 왜 수소 원자 스펙트럼은 불연속이며 규칙성이 나타나는지는 밝혀내지 못했다.
41) 보어 수소 원자 모형
이러한 분광학자들의 궁금증과 러더퍼드의 고민을 해결한 사람은 닐스 보어이다. 보어의 대략적인 생각은 이러하다. 태양광이나 흑체 복사는 거시 세계에 해당하는 현상으로 '상식적인' 물리 법칙에 잘 들어맞게 연속적인 스펙트럼을 나타낸다. 그러나 수소 원자는 미시 세계에 해당하는 대상으로 수소 원자가 내는 빛은 고전적인 물리 법칙을 벗어나는 것이 가능하지 않을까라는 것이다. 앞서 아인슈타인이 광양자 이론을 제시함으로써 빛은 최소 에너지 단위를 가지는 광양자들로 이루어져서 '양자화'되어 있다는 사실이 알려졌다. 빛이 양자화되어 있다면, 전자라고 그렇지 않을 이유가 있냐는 것이다.

1913년 보어는 새로운 원자 모형을 발표하게 되는데, 그는 전자는 오직 정해진 각운동량과 에너지를 갖는 특정한 준위의 궤도만 돌 수 있다고 가정했다. 특정 궤도에는 그에 해당하는 에너지가 존재하고, 궤도를 도는 전자는 그 에너지를 가진 채로 계속 운동한다. 즉 전자가 서로 다른 궤도 사이를 오고 갈 때만 빛의 형태로 에너지가 흡수 및 방출된다. 따라서 에너지 보존에 의해 전자가 갖는 서로 다른 두 에너지 준위의 차는 Figure 2와 같이
$$E_f - E_i = h\nu$$로 주어진다. 전자가 에너지 준위 사이를 이동할 때 빛의 형태로 에너지가 나오고, 그 값은 광양자 한 개의 에너지인 것이다. 이를 '진동수 조건'이라고 부른다.
또한 전자 각운동량 $L_n$은 다음과 같이 주어진다.
$$L_n = m_e v r_n = n\frac{h}{2 \pi} ( = n\hbar) (n = 1, 2, ...)$$ 이때 질량이 $m_e$인 전자가 반지름이 $r_n$인 궤도를 $v$의 선속도로 움직인다고 생각한다. 각운동량이 양자화되어 있으므로 전자는 특정 궤도에서 안정된 상태를 유지한다. 따라서 이 궤도를 보어의 '정상궤도'(Stationary orbit)라고 부른다. 이를 '각운동량 조건'이라고 부른다.
이러한 가정 하에 수학적으로 기술해보자. 핵과 전자 사이의 전기력이 구심력으로 작용하는 것은 마찬가지이므로,
$$\frac{1}{4 \pi \epsilon_0} \frac{e^2}{r^2_n} = m_e \frac{v^2}{r_n}$$이 성립한다. 이때
$$L_n = m_evr_n = n\frac{h}{2\pi} \\ \Longrightarrow v = \frac{nh}{2m_e r_n \pi} $$이므로 $v$를 위 식에 대입해서 $r_n$에 대해 정리하면 다음과 같다.
$$r_n = \frac{\epsilon_0 n^2 h^2}{\pi m_e e^2} (n = 1, 2, ...)$$ 따라서 양자화된 궤도들 사이의 관계식을 얻는다.
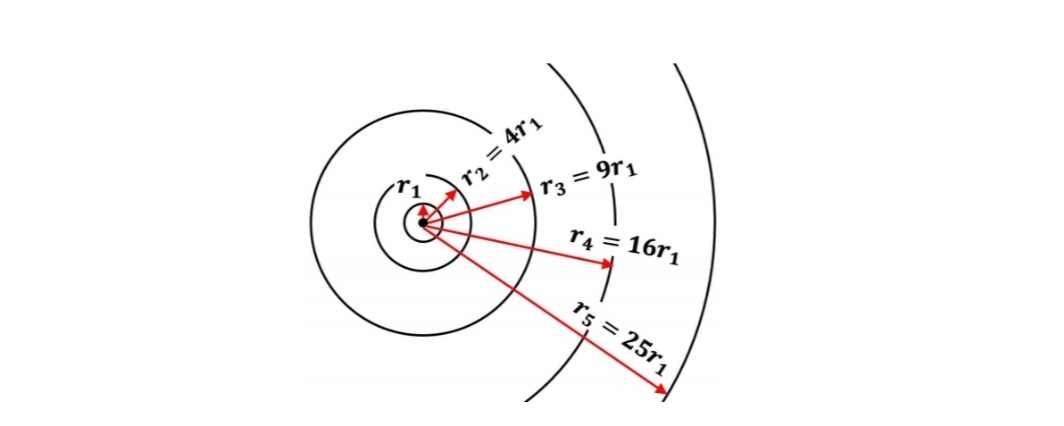
에너지 역시 비슷하게 기술하면, 전자의 총에너지 $E_n$는
$$E_n = \frac{1}{2}m_ev^2 - \frac{1}{4 \pi \epsilon_0} \frac{e^2}{r_n}$$으로 주어지고, 앞에서 구한 $v$와 $r_n$을 대입해서 정리하면
$$E_n = - \frac{m_e e^4}{8 \epsilon^2_0 n^2 h^2} (n = 1, 2, ...)$$이다. 즉 전자의 총에너지는 양자화된다.
앞서 진동수 조건에서 $E_f - E_i = h\nu = h \frac{c}{\lambda}$로 주어졌다. 서로 다른 준위 $n_1$와 $n_2$ 사이의 에너지 차이를 위 식을 통해 나타내고, 리드버그 공식과 동일한 형태로 정리하면 다음과 같다.
$$E_{n_2} - E_{n_1} = -\frac{m_e e^4}{8 \epsilon^2_0 n^2_2 h^2} + \frac{m_e e^4}{8 \epsilon^2_0 n^2_1 h^2} = h \frac{c}{\lambda} \\ \Longrightarrow \frac{1}{\lambda} = \frac{m_e e^4}{8 \epsilon^2_0 h^3 c} (\frac{1}{n^2_1} - \frac{1}{n^2_2})$$ 이때 괄호 앞의 값을 구하면 $1.0973 \cdot 10^7 m^{-1}$이고, 이 값은 리드버그 상수 $R_H$와 거의 같다. 즉 실험적 결과로부터 분광학자들이 짜 맞춘 공식과 보어가 가정으로부터 수학적으로 도출한 공식과 동일하다는 것이다. 따라서 보어의 가정은 타당하다고 볼 수 있으므로 원자를 제대로 기술하기 위해서는 각운동량과 에너지가 양자화되어 있어야 한다.
러더퍼드의 원자 모형은 전자가 핵 주위를 돌 때 궤도의 반경이 연속적이기 때문에 문제에 부딪혔다. 그러나 보어의 모형은 궤도가 양자화되어 있으므로 러더퍼드의 고민 자체가 성립하지 않는다고 정해버린 것이다. 또한 특정 궤도에만 전자가 존재할 수 있기 때문에 수소 원자의 불연속적인 스펙트럼 또한 설명이 된다. 그러나 보어의 원자 모형 또한 수소 외의 다른 원자에 대해서는 잘 들어맞지 않는다는 문제점이 남아있었다.