42) 프랑크-헤르츠 실험
프랑크(J. Franck)-헤르츠(G. Hertz) 실험은 보어의 원자 모형에서 가정한 전자의 에너지의 양자화를 실험적으로 확인시켜준 실험이다. 실험 장치는 Figure 1-(a)와 같다.
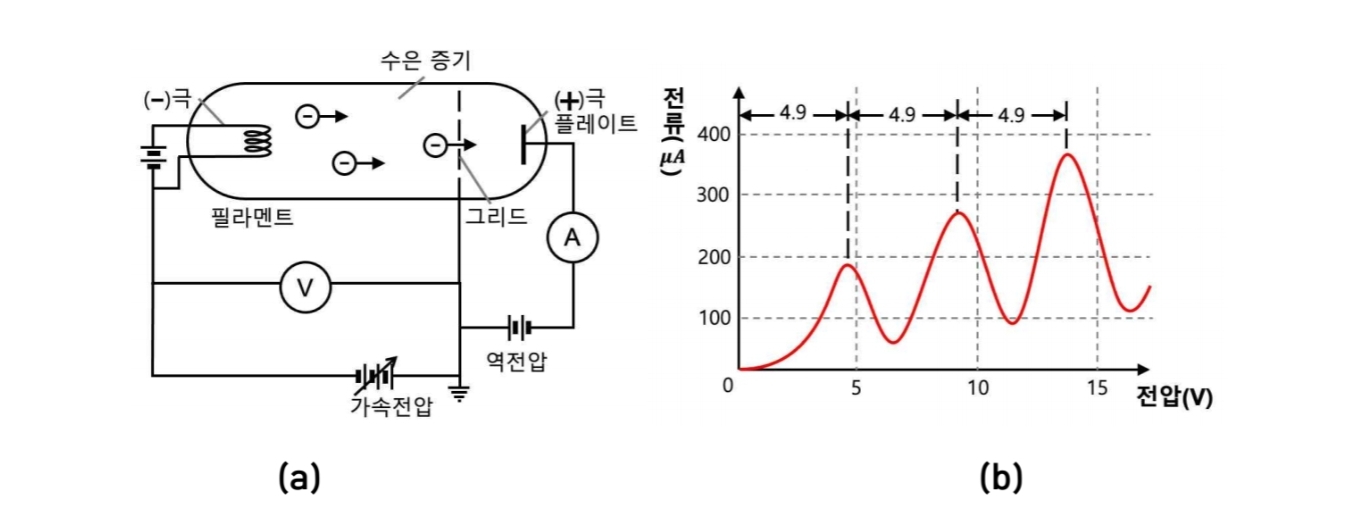
기본적으로 실험 장치는 수은 증기가 들어있는 가이슬러관1에 열전자가 튀어나오는 필라멘트와 열전자를 가속시키는 그리드, 그리고 그리드를 통과한 전자들을 수집하는 플레이트(양극)로 구성된다. 그리드는 필라멘트에 대해 (+) 전위를 가지며 가속전압 $V$의 크기를 바꿀 수 있다. 플레이트((+)극)는 그리드에 대해 전위가 낮아서 역전압 $V_0$가 걸린다. 따라서 그리드를 통과한 전자는 속도가 줄어들어 플레이트에 모여들어 전류의 형태로 나타난다. 그리드와 플레이트 사이에 역전압을 걸어주는 이유는, 전류를 제한해서 어떤 최솟값을 넘는 에너지를 갖는 전자들만 플레이트에 도달하게 함으로써 Figure 1-(b)와 같은 보다 깨끗한 전류-전압 곡선을 얻기 위함이다.
가속전압 $V$를 크게 함으로써 필라멘트에서는 더 많은 전자가 튀어나와 전류의 세기가 증가한다. 만일 전자가 수은 증기에 있는 원자와 탄성 충돌을 한다면 그 과정에서 운동 에너지의 손실 없이 운동 방향만 바뀔 것이다. 따라서 플레이트에 들어오는 전자의 수는 거의 변동이 없을 것이고, 전류는 이전의 기조를 유지할 것이다.
그러나 전자가 수은 원자와 충돌하는 과정에서 수은 원자를 들뜨게 하는데 운동 에너지의 일부를 사용한다면, 즉 비탄성 충돌을 한다면 속도가 줄어들어 플레이트에 도달하는 전자의 수가 줄어들 것이고, 전류도 감소한다. 가속전압을 조절하는 과정에서 이러한 일이 일어난다면 전류-전압 곡선이 순간적으로 감소하는 전압값이 존재할 것이고, 실제로 실험을 수행하면 Figure 1-(b)처럼 주기적으로 감소하는 곡선을 얻을 수 있다. 이때 그 주기는 4.9$V$로, 즉 수은 원자는 $\Delta E = 4.9eV$에 해당하는 에너지 준위를 가지고 있음을 알 수 있다. 만약 수은 원자가 연속적인 에너지를 가질 수 있다면 이와 같은 실험 결과와는 상충되며, 따라서 수은 원자는 보어의 원자 모형에서 가정한 것과 같이 불연속적인 에너지 준위, 즉 양자화된 에너지를 가지고 있다고 해석된다.
실제로 들뜬 수은 원자는 $\lambda = 253.6 nm$의 빛을 발생시키는데, 이를 $E = hf = h \frac{c}{\lambda}$에 넣어 계산하면 $E = 4.9eV$라는 값으로 실험 결과와 정확히 일치한다. 따라서 프랑크-헤르츠 실험은 보어 모형을 가정하지 않고는 설명할 수 없는 결과를 보여주며, 보어의 원자 모형에 더욱 타당성을 부여하는 실험이라고 할 수 있다.
43) 조머펠트의 원자모형
프랑크-헤르츠 실험과 같은 결과에도 불구하고, 보어의 원자 모형은 몇 가지 문제점들이 있었다. 나열하면 다음과 같다.
1. 수소 원자만 설명 가능: $He, Ne$와 같은 다전자 기체 원자에서는 잘 맞지 않는다.
2. 제만 효과(Zeeman effect): 제만 효과를 설명할 수 없다. 제만 효과는 자기장 속에서 원자의 선 스펙트럼이 갈라지는 현상으로, 1897년 제만(P. Zeeman)이 발견했다.
3. 슈타르크 효과(Stark effect): 슈타르크 효과를 설명할 수 없다. 슈타르크 효과는 수소 원자가 전기장 속에서 선 스펙트럼이 갈라지는 현상으로, 1913년 슈타르크(J. Stark)가 발견했다.
4. 미세구조(Fine structure): 수소 원자에서 미세구조가 나타나는 현상을 설명할 수 없다. 미세구조란 수소의 발머계열 선 스펙트럼에서 하나의 파장인 줄 알았던 스펙트럼선이 아주 미세하게 분리된 2개의 파장으로 되어있는 현상을 말한다.
이에 조머펠트(A. Sommerfeld)는 전자가 2차원 원운동을 하는 것이 아니라, 하나의 변수(양자수)를 더 도입하여 3차원으로 타원 운동을 한다고 가정하게 된다. 또한 상대성이론 또한 고려하였는데, 이러한 가정들이 더욱 일반적이라는 것이다. 보어의 원자 모형에서 원 궤도는 $1, 2, 3, ...$ 등의 자연수들을 값으로 가지는 변수 $n$에 의해 결정되는데, 타원 궤도는 장축 방향과 단축 방향을 각각 표현하기 위해 2개의 변수, 즉 양자수가 필요하게 된다. 따라서 궤도의 크기(반지름) 뿐만 아니라 방향을 결정해 주는 변수가 하나 더 필요하고, 양자화 조건이 하나 더 필요하게 된다.
따라서 조머펠트는 원자 내의 전자의 상태는 세 개의 양자수 $n, k, m$로 나타내어지고, 각각 '주양자수'(Principal quantum nubmer), '부양자수'(Subordinate quantum number), 그리고 '자기 양자수'(Magnetic quantum number)라고 불렀다. 또한 일반화된 양자화 조건인
$$\oint p_i dp_i = n_ih$$을 가정하고 이를 '조머펠트 양자화 조건'으로 불렀다. 여기서 $p_i$는 일반화된 운동량으로 일반화된 좌표인 $dq_i (= x, y, z, r, \theta, \phi)$에 해당하는 운동량이고, $n_i$는 일반화된 좌표에 대응되는 정수를 나타낸다. 이 조건으로 그는 소수 원자의 에너지와 각운동량의 양자화를 증명해 내었다. 이러한 원자 모형을 '조머펠트 원자 모형', 혹은 '보어-조머펠트 원자 모형'이라고 부른다.

이러한 조머펠트의 원자 모형은 앞서 상술한 보어 원자 모형의 문제점 2~4번을 설명할 수 있었으나 각운동량의 양자화, 다전자 원자 문제 등을 해결할 수 없었다. 이후 슈뢰딩거 방정식이 등장하면서 조머펠트 원자 모형은 자연스럽게 사라지게 된다.
- 양쪽에 두 개의 전극을 넣은 반영구적 진공유리관 [본문으로]