Isomorphism

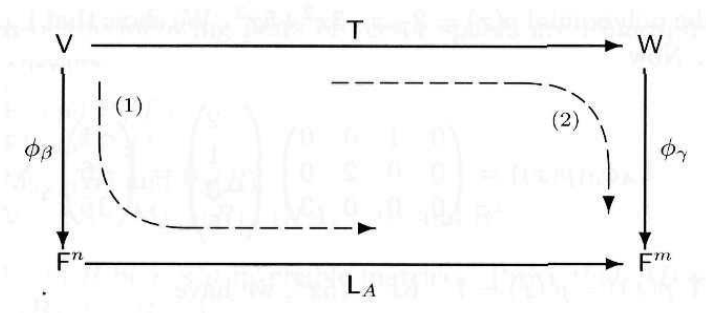
    이 포스트에서 $V, W$는 모두 $F$-벡터공간으로 취급한다.

Inverse of a matrix

Definition 1. Let $A \in M_{n \times n}(F)$. Then $A$ is invertible if $\exists B \in M_{n \times n}(F)$ such that $AB = BA = I_n$. The matrix $B$ is called the inverse of $A$ and is denoted by $A^{-1}$.

Isomorphism

Definition 2. We say that $V$ and $W$ are isomorphic, denoted $V \cong W$, if $\exists T \in \mathcal{L}(V, W)$ such that $T$ is invertible. Such $T$ is called an isomorphism from $V$ onto $W$.

    벡터공간 $V$와 $W$ 사이에 전단사 선형 변환 $T$가 존재한다는 것은 두 공간의 벡터 사이에 어떤 대응이 존재한다는 뜻이고, 연산이 보존된다는 말과 같다. 따라서 두 공간은 수학적으로 동일한 성질을 가지는 것으로 간주할 수 있고, 이때 두 공간은 isomorphic하다고 부른다. 

Theorem 1

Theorem 1. Let $T \in \mathcal{L}(V, W)$ be an isomorphism. Then $T^{-1}: W \rightarrow V$ is linear.

Proof. Since $T$ is invertible, $T$ is surjective. Then for $x, y \in V$, $\exists u, v \in W$ such that $T(x) = u, T(y) = v \Longleftrightarrow T^{-1}(u) = x, T^{-1}(v) = y$. For a scalar $c$, $cT(x) + T(y) = T(cx + y) = cu + v \Longleftrightarrow T^{-1}(cu + v) = cx + y = cT^{-1}(u) + T^{-1}(v).$ Hence $T^{-1}$ is linear. $\blacksquare$

    두 공간이 isomorphic하면 isomorphism을 통해 두 공간 사이의 많은 수학적 대상들이 보존된다. 지금부터 보존하는 대상들을 하나씩 살펴보자. 

Theorem 2 

Theorem 2. $V \cong W$ $\Longleftrightarrow$ dim($V$) = dim($W$). 

Proof. Let $T$ be an isomorphism from $V$ onto $W$. Then rank($T$) = dim($W$) = dim($V$). by Theorem 2. $\blacksquare$

Theorem 3

Theorem 3. Let $T \in \mathcal{L}(V, W)$ and let $\beta, \gamma$ be finite ordered bases for $V, W$, respectively. Then $T$ is invertible $\Longleftrightarrow$ $[T]_{\beta}^{\gamma}$ is invertible. Furthermore, $[T^{-1}]_{\gamma}^{\beta} = ([T]_{\beta}^{\gamma})^{-1}$.

Proof. 
($\Longrightarrow$)
$[T]_{\beta}^{\gamma}[T^{-1}]_{\gamma}^{\beta} = [TT^{-1}]_{\gamma} = [I_W]_{\gamma} = I.$ Similarlly, $[T^{-1}]_{\gamma}^{\beta}[T]_{\beta}^{\gamma} = I.$ Hence $[T]_{\beta}^{\gamma}$ is invertible, and $[T^{-1}]_{\gamma}^{\beta} = ([T]_{\beta}^{\gamma})^{-1}.$
($\Longleftarrow$)
Since $[T]_{\beta}^{\gamma}$ is invertible, $\exists$ a matrix $A$ such that $A[T]_{\beta}^{\gamma} = I$, where $A = ([T]_{\beta}^{\gamma})^{-1}$.
Suppose that $T(x) = T(y)$ for $x, y \in V$. Then we have $A[T]_{\beta}^{\gamma}[x]_{\beta} = I[x]_{\beta} = [I_V]_{\beta}[x]_{\beta} = [x]_{\beta}$. On the other hand, $A[T]_{\beta}^{\gamma}[x]_{\beta} = A[T(x)]_{\gamma} = A[T(y)]_{\gamma} = A[T]_{\beta}^{\gamma}[y]_{\beta} = [y]_{\beta}$. Thus $[x]_{\beta} = [y]_{\beta} \Longleftrightarrow x = y$, i.e., $T$ is injective.
Since $[T]_{\beta}^{\gamma}$ is invertible, it is square. This means that $\beta$ and $\gamma$ contain the same number of vectors. Thus $T$ is surjective. Hence $T$ is bijective. $\blacksquare$

Corollary 1. Let $A \in M_{n \times n}(F)$. Then $A$ is invertible $\Longleftrightarrow$ $\mathsf{L}_A$ is invertible. Furthermore, $(\mathsf{L}_A)^{-1} = \mathsf{L}_{A^{-1}}.$

Theorem 4

Theorem 4. Let $T \in \mathcal{L}(V, W)$, and let $\beta = \{v_1, ..., v_n\}$ be an ordered basis for $V$. Then $T$ is an isomorphism $\Longleftrightarrow$ $T(\beta)$ is a basis for $W$.

Proof. 
($\Longrightarrow$) Note that $T(\beta)$ generates $R(T) = W$. Suppose that $\sum_{i=1}^n a_iT(v_i) = \mathbf{0}$ for $a_i \in F (i = 1, ..., n)$. Then we have $T(\sum_{i=1}^n a_iv_i) = \mathbf{0}$. Note that $T$ is injective, so $N(T) = \{\mathbf{0}\}$. Thus $\sum_{i=1}^n a_iv_i = \mathbf{0} \Longrightarrow a_i = 0 (i = 1, ..., n)$. Hence $T(\beta)$ is a basis for $W$. 
($\Longleftarrow$) Suppose that $T(x) = T(y)$ for $x, y \in V$. Let denote $x = \sum a_iv_i$ and $y = \sum b_iv_i$ for $a_i, b_i \in F$. Then we have $\sum a_iT(v_i) = b_iT(v_i) \Longrightarrow \sum (a_i - b_i)T(v_i) = \mathbf{0} \Longrightarrow a_i = b_i$ for all $i$. Thus $x = y$, so $T$ is injective.
$\forall y \in W$, let denote $y = \sum c_iT(v_i)$ for $c_i \in F$. Then $y = T(\sum a_iv_i)$. Thus $y \in R(T)$. Since $R(T) \subseteq W$, $R(T) = W$, so $T$ is surjective. This means that $T$ is bijective, i.e., an isomorphism. $\blacksquare$

Theorem 5

Theorem 5. Let $T \in \mathcal{L}(V, W)$ be an isomorphism, and let $V_0 \leq V$. Then
(1) $T(V_0) \leq W$,
(2) dim($V_0$) = dim($T(V_0)$).

Proof. 
(1) Let $x, y \in T(V_0)$. Then $\exists a, b \in V_0$ such that $T(a) = x, T(b) = y$
$\Longrightarrow cx + y = cT(a) + T(b) = T(ca + b) \in T(V_0)$. Thus $T(V_0) \leq W$.
(2) Define $T': V_0 \longrightarrow T(V_0)$ by $T'(v) = T(v), \forall v \in V_0$. Then cleary $T'$ is an isomorphism. Thus dim($V_0$) = dim($T(V_0)$) by Theorem 2. $\blacksquare$

    이처럼 $T$가 isomorphism이면, $T$는 두 공간 사이의 차원(Theorem 2), 기저(Theorem 4), 부분공간(Theorem 5)을 보존한다는 사실을 알 수 있다. 

---

Reference is here: https://product.kyobobook.co.kr/detail/S000003155051

Linear Algebra | Stephen Friedberg - 교보문고