이 포스트에서 $V, W$는 모두 $F$-벡터공간으로 취급한다.
Theorem 1 (The Fundamental Theorem of Linear Algebra)
Theorem 1. Let dim($V$) = $n$ and dim($W$) = $m$, and let $\beta, \gamma$ be ordered bases for $V, W$, respectively. Then the function $\Phi: \mathcal{L}(V, W) \rightarrow M_{m \times n}(F)$, defined by $\Phi(T) = [T]_{\beta}^{\gamma}$ for $\forall T \in \mathcal{L}(V, W)$, is an isomorphism.
Proof.
(1) $\Phi$ is linear: By Theorem 1, it is clear.
(2) $\Phi$ is an isomorphism: By Theorem 1, it is clear that $\Phi$ is injective. Let $A \in M_{m \times n}(F)$, and let $\beta = \{v_1, ..., v_n\}, \gamma =\{w_1, ..., w_m\}$ be ordered bases for $V, W$, respectively. Then $! \exists T \in \mathcal{L}(V, W)$ such that $T(v_j) = \sum_{i = 1}^m A_{ij}w_i (j = 1, ..., n).$ $\Longrightarrow [T]_{\beta}^{\gamma} = A$. Thus $\Phi(T) = A$, so $\Phi$ is surjective. This means that $\Phi$ is bijective, i.e., an isomorphism. $\blacksquare$
Corollary
Corollary. Let dim($V$) = $n$ and dim($W$) = $m$. Then dim($\mathcal{L}(V, W)$) = $mn$.
Proof. Since $\mathcal{L}(V, W) \cong M_{m \times n}(F)$, dim($M_{m \times n}(F)$) = $mn$ = dim($\mathcal{L}(V, W)$). $\blacksquare$
Remark
Remark. Let dim($V$) = $n$ and dim($W$) = $m$, and let $\beta, \gamma$ be ordered bases for $V, W$, respectively. Let $T \in \mathcal{L}(V, W)$, and define $A := [T]_{\beta}^{\gamma}$.
Notice that there are two composites of linear transformations $L_A\phi_{\beta}$ and $\phi_{\gamma}T$ that map $V$ into $F^m$, respectively.
We may conclude that
$$L_A\phi_{\beta} = \phi_{\gamma}T.$$ ($\because$) $\forall x \in V,$
$$(L_A\phi_{\beta})(x) = L_A(\phi_{\beta}(x)) = L_A([x]_{\beta}) = A[x]_{\beta} \\ = [T]_{\beta}^{\gamma}[x]_{\beta} = [T(x)]_{\gamma} = \phi_{\gamma}(T(x)) = (\phi_{\gamma}T)(x).$$ Hence $L_A\phi_{\beta} = \phi_{\gamma}T.$
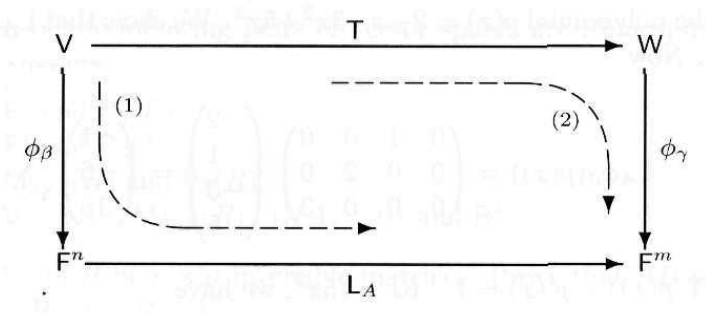
$T$가 $\mathcal{L}(V, W)$에 속하는 선형 변환일 때, $T$는 주어진 벡터 $v \in V$를 벡터 $w = T(v) \in W$로 변환시키는 역할을 한다. 선형대수학의 기본정리는 선형 변환 $T$와 $T$의 행렬 표현 $[T]_{\beta}^{\gamma}$가 사실상 수학적으로 동일한 대상이라고 말해준다. 즉 $v$를 $w$로 변환하는 과정에서 $T$를 $[T]_{\beta}^{\gamma}$로 대체해도 그 변환의 결과가 동일하다는 것이다.
다만 $v$에 $[T]_{\beta}^{\gamma}$를 작용시킨다는 것을 수학적으로 표현하기 위해서는, 다시 말해 행렬의 곱셈이 정의되기 위해서는 자연스럽게 $v$가 $F^n$에 속하는 열벡터여야 할 것이다. 따라서 $v$의 좌표벡터를 사용하는 것이 자연스럽다.
결과를 요약하면 식 $T(v) = w$는 $[T(v)]_{\gamma} = [T]_{\beta}^{\gamma}[v]_{\beta}$과 동일해야 함을 알 수 있고, 실제로도 Theorem 3을 통해 동일하다는 것을 확인할 수 있다. 이것을 요약한 것이 위 Remark의 내용이다.