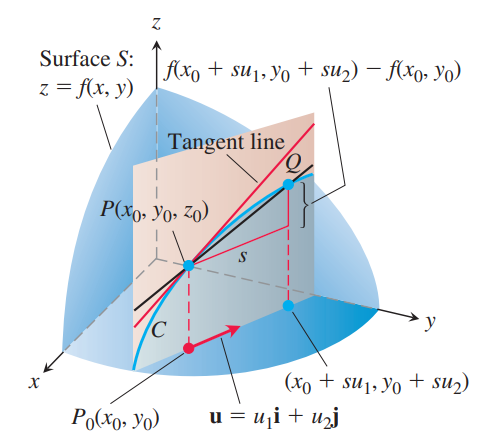
Directional DerivativeDefinition 1. The derivative of $f$ at $P_0 (x_0, y_0)$ in the direction of the unit vector $\mathbb{u} = u_1 \mathbb{i} + u_2 \mathbb{j}$ is the number $$\left( \frac{df}{ds} \right)_{\mathbb{u}, P_0} = \lim_{s \to 0} \frac{f(x_0 + su_1, y_0 + su_2) - f(x_0, y_0)}{s},$$ provided the limit exists. It is also denoted by $$D_{\mathbb{u}}f(P_0) \text{  or  } D_{\mathbb{u}}f \b..

Theorem 1Theorem 1. Suppose that $F(x, y)$ is differentiable and that the equation $F(x, y) = 0$ defines $y$ as a differentiable function of $x$. Then at any point where $\partial_y F \neq 0,$ $$\frac{dy}{dx} = - \frac{\partial_x F}{\partial_y F}.$$Proof. Since $F(x, y) = 0$, the derivative $\frac{dF}{dx}$ must be zero. By the Chain Rule, we find $$0 = \frac{dF}{dx} = \frac{\partial F}{\partial ..

Theorem 1Theorem 1. If $w=f(x, y)$ is differentiable and if $x = x(t), y=y(t)$ are differentiable functions of $t$, then the composition $w=f(x(t), y(t))$ is a differentiable function of $t$ and $$\frac{dw}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}.$$Proof. Let $\Delta x, \Delta y$ and $\Delta w$ be the increments that result from changing $t..

Partial DerivativeDefinition 1. The partial derivative of $f(x, y)$ with respect to $x$ at the point $(x_0, y_0)$ is $$\frac{\partial f}{\partial x} \Bigg|_{(x_0, y_0)} = \lim_{h \to 0} \frac{f(x_0 + h, y_0) - f(x_0, y_0)}{h},$$ provided the limit exists. The partial derivative with respect to $y$ is defined in the same way.특정 변수를 상수로 취급하고 한 변수만 다룬다는 의미에서 편미분이라고 말한다. 기호로는 $\frac{\partial f}{\par..

프로그램(Program)은 일종의 명령어 집합이다. 컴퓨터에서 특정 기능을 수행하도록 프로그램을 만들기 위해서는 이 명령어들을 구조와 논리에 맞게 작성해 주어야 한다. 이때 우리는 다양한 프로그래밍 언어를 사용해 코드(code)를 작성하고, 이러한 행위를 코딩(coding)이라고 부른다.     프로그래밍 언어라고 하면 대부분 python, C, C++, Java 등을 떠올릴 것이다. 이와 같은 언어들을 고급 언어(High Level Language)라고 하고, 이와 구분되는 언어로 저급 언어(Low Level Language)가 있다. 고급, 저급과 같은 말의 뉘앙스 때문에 오해할 수도 있지만 두 언어는 단지 사용자 친화적인지, 컴퓨터 친화적인지에 따라 구분된다. 컴퓨터가 더 이해하기 쉬운 언어면 저급..

컴퓨터에서 문자를 처리하려면 당연하게도 컴퓨터가 이해할 수 있는 언어로 (2진수, 8진수, 16진수 등등...) 변환하여야 한다. 그렇다면 각 문자들에 서로 다른 값들을 할당해 주어야 하고, 이를 정리한 문자표가 필요할 것이다. 이처럼 값이 할당되어서 컴퓨터가 이해하고 처리할 수 있는 문자들을 모아놓은 모음을 문자 집합(Character Set)이라고 한다.     문자 집합에 속한 문자를 컴퓨터가 처리할 수 있게 변환하는 과정을 문자 인코딩(Character Encoding), 그 반대의 과정을 문자 디코딩(Character Decoding)이라고 한다. 과거부터 지금까지 다양한 문자 집합과 인코딩, 디코딩 방법이 제안되었고, 그 중 몇 가지를 살펴보도록 하자. 아스키 코드    초창기 컴퓨터는 아스키..

부동소수점컴퓨터에서는 실수를 '부동소수점'(Floating Point Number) 형식으로 저장한다. '부동'(Floating)이라는 표현은 배가 물에 떠서 이리저리 움직이듯이 소수점의 위치를 하나로 고정시키지 않고 움직인다는 뜻이다. 예컨대 $352.45$라는 10진수 실수를 $3.5245 \times 10^2$의 형식으로 나타나는 것을 '정규화'(Normalization)한다고 말하며, 이와 같이 정규화하여 나타낸 실수 표현을 부동소수점 형식이라 말한다.    실수를 부동소수점 형식으로 표현하면 매우 크거나 작은 숫자를 비교적 간단하게 표현할 수 있고, 다소 한정된 비트만을 가지고 정밀하게 숫자를 표현할 수 있다는 장점이 있기 때문에 컴퓨터는 부동소수점 형식으로 실수를 저장한다.    부동소수점 형..

Algorithm 1 (8진수)Algorithm 1 (8진수). 1. 임의의 2진수를 소수점을 기준으로 좌우 3자리씩 분할한다.2. 분할한 단위를 10진수로 변환한다.3. 변환한 10진수를 8진수로 변환한다.예를 들면 $11010.1010$라는 2진수가 있다고 하자. 이때 위 알고리즘의 1번을 수행하면 결과물은 다음과 같다. $$11 / 010. 101 / 0$$ 이제 $11$을 10진수로 변환하면 $3$이고, $010$은 $2$, $101$은 $5$, $0$은 $0$이다. 10진수로 변환한 각 숫자를 다시 8진수로 변환하면 각각 $3, 2, 5, 0$이므로 변환된 8진수는 $32.5$이다.  Algorithm 2 (16진수)Algorithm 2 (16진수). 1. 임의의 2진수를 소수점을 기준으로 좌우..

Definition. 컴퓨터는 원하는 결과를 얻기 위해 입력기능을 이용하여 데이터를 디지털로 변환하고 처리, 저장 기능을 이용하여 데이터를 처리하며, 변환된 정보를 출력기능을 이용하여 적절한 출력장치로 출력할 수 있는 전자적으로 계산을 수행하는 장치이다. 장황하게 정의를 늘어놓았지만 결국 핵심은 계산이고, 계산은 다시 말해 명령어(Instruction) 처리와 같다고 말할 수 있다. 컴퓨터의 기원을 거슬러 올라가다보면 주판에 다다르게 되는데, 즉 인간은 복잡하고 많은 양의 계산을 처리하기 위해 컴퓨터라는 기계를 점점 발전시켜 왔다고 볼 수 있다. 컴퓨터는 크게 중앙처리장치(CPU: Central Processing Unit), 주기억장치(Main Memory, or Memory), 보조기억장치, 입출력장..

[본 독서인증은 스노우폭스북스의 지원을 받아 작성되었습니다.] "출판인이라 '출판'으로 말합니다"라는 문장이 나를 뒤흔든다. 나는 무엇으로 말할 수 있는가? 그저 시류에 몸을 맡기고 숨 죽여 살아가는 한 사람이 되지 않으리라!https://product.kyobobook.co.kr/detail/S000215011709 선과 악의 기준은 무엇인가? | 돈 후안 마누엘 - 교보문고선과 악의 기준은 무엇인가? | 출판도 책에 인쇄된 ‘글’로 시대정신에 참여 최초 출간일 1335년 스페인 알폰소 10세 국왕의 친조카 48편의 선과 악을 가려보는 어른 동화이 책은 표지와 본문 제product.kyobobook.co.kr