Curl and Divergence

Curl

물과 같은 유체가 어떤 평면 위에서 흐르고 있는 물리적인 상황을 상상해보자. 이때 위치에 따른 유체의 속도를 나타내는 벡터장을 $\mathbf{F}(x, y)$라고 하자. 이때 평면 상의 어떤 점에서 유체가 어느 방향으로 얼마나 회전하고 있는지 그 정도를 나타내는 물리량을 측정하려고 한다.

 

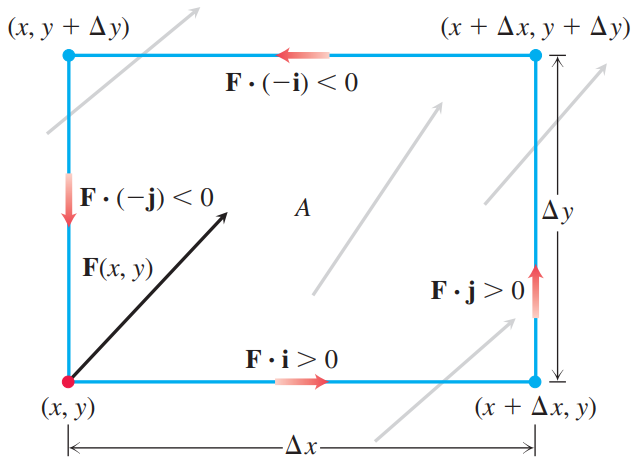
우선 다음과 같이 주어진 작은 rectangular region $A$를 고려하자.

Thomas Calculus 14e 954p.

$A$는 임의의 점 $(x, y)$를 꼭짓점으로 하고 각 변의 길이를 $\Delta x, \Delta y$로 갖는다. 구하고자 하는 물리량은 면적의 테두리와 counterclockwise한 방향을 갖는 사각형 모양 closed curve에서의 circulation으로부터 얻을 수 있다고 생각할 수 있다. 따라서 circulation을 구해보자.

 

각 모서리가 $x, y$축에 평행하고 $\mathbf{F}$의 component인 $M, N$은 주어진 영역에서 모두 양수라고 가정하자. 먼저 아래쪽 모서리에서 circulation은 다음과 같다. $$\int_{\text{bottom}} \mathbf{F} \cdot d \mathbf{r} = \int_{x}^{x + \Delta x} M(x', y) dx'$$ 이때 mean value theorem of definite integral의 의해 $$\int_x^{x + \Delta x} M(x', y) dx' = M(a, y) \cdot \Delta x$$ 를 만족하는 상수 $a$가 $[x, x + \Delta x]$에 존재한다.

 

우리는 주어진 점 $(x, y)$을 생각하고 있으므로, 최종적으로 $\Delta x, \Delta y \to 0$인 상황을 상정할 것이다. 즉 $a = x$라고 두고 approximate하자. 따라서 아래쪽 모서리에서 circulation은 $M(x, y) \Delta x$이다. 같은 논리를 적용해 각 모서리에서 circulation을 계산하면 다음과 같다: $$\begin{align} &\text{bottom}: \quad M(x, y) \Delta x \\ &\text{top}: \quad -M(x, y + \Delta y) \Delta x \\ &\text{left}: \quad -N(x, y) \Delta y \\ &\text{right}: \quad N(x + \Delta x, y) \Delta y \end{align}$$ 이렇게 둔 이유는 계산의 편의를 위해서이다. 

 

이제 위에서 구한 값들을 같은 축의 값끼리 더해주면 다음과 같다: $$\begin{align} &\text{bottom and top}: \quad  -(M(x, y + \Delta y) - M(x, y)) \Delta x \approx -\left( \frac{\partial M}{\partial y} \Delta y \right) \Delta x \\ &\text{left and right}: \quad (N(x + \Delta x, y) - N(x, y)) \Delta y \approx \left( \frac{\partial N}{\partial x} \Delta x \right) \Delta y \end{align}$$ 위에서 언급한대로 $\Delta x, \Delta y \to 0$을 상정하므로 위와 같은 근사가 성립한다. 따라서 이 값들을 모두 더해주면 최종적으로 $A$에서의 circulation이 되고, 그 값은 $$\left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) \Delta x \Delta y$$ 이다. 

 

우리는 점 $(x, y)$에서 유체가 얼마나 회전하고 있는지를 측정해야 하므로 위에서 구한 값에 region $A$의 넓이 $\Delta x \Delta y$를 나눠주면 그 값은 $$\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}$$ 이고, 이 값을 circulation density, 혹은 curl이라고 부른다.

Definition 1. The circulation density at the point $(x, y)$ of a vector field $\mathbf{F}(x, y) = \langle M(x, y), N(x, y) \rangle$ with the continuous first partial derivatives is $$\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}.$$ This expression is also called the $\mathbf{k}$-component of the curl, denoted by $(\nabla \times \mathbf{F}) \cdot \mathbf{k}$.

$(\nabla \times \mathbf{F}) \cdot \mathbf{k}$라는 표기법에서 알 수 있듯이, 이 값이 양수이면 $\nabla \times \mathbf{F}$는 $+z$축 방향이고, 음수이면 그 반대 방향이다. 

 

이 값을 통해 회전의 방향을 측정하려고 했었다. 위의 유도 과정에서 우리는 closed curve의 방향을 counterclockwise로 잡았었다. 유체가 curve와 동일한 방향, 즉 반시계방향으로 회전한다면 circulation은 양수일 것이고, 따라서 $(\nabla \times \mathbf{F}) \cdot \mathbf{k}$의 값도 양수일 것이다. 이를 통해 회전의 방향을 파악할 수 있다. 

 

위의 논의는 $xy$ 평면 상, 다시 말해 $z$축과 평행한 축의 방향으로 회전하고 있는 상황이다. 동일한 유도 과정을 $x, y$ 축 방향으로도 생각할 수 있으므로 일반적으로 curl은 다음과 같이 정의한다.

Definition 2. Let $\mathbf{F} = \langle M, N, P \rangle$ be a vector field with continuous first partial derivatives. Then the curl of $\mathbf{F}$ is the vector $$\Big\langle \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z}, \frac{\partial M}{\partial z} - \frac{\partial P}{\partial x}, \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \Big \rangle.$$ We denote this $\nabla \times \mathbf{F}.$

$\nabla$를 $$\Big \langle \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \Big \rangle$$ 과 같은 벡터로 기억하면 $\nabla \times \mathbf{F}$는 $$\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ M & N & P \end{vmatrix}$$ 와 같은 행렬식으로 기억할 수 있다.

Divergence

이번에는 주어진 점 $(x, y)$에서 유체가 얼마나 유출되고 있는지, 혹은 유입되고 있는지를 측정하고자 한다. 마찬가지로 아래와 같은 영역 $A$를 고려하자.

Thomas Calculus 14e 957p.

회전과는 다르게 유출 혹은 유입이므로 벡터장 $\mathbf{F}$의 영역 $A$의 각 모서리에 대해서 수직한 방향의 성분을 취해야 한다. 이때 방향은 $A$의 테두리 안에서 밖으로 향하는 쪽을 선택한다. 이를 통해 우리가 구하고자 하는 물리량은 각 모서리에 대한 flux를 계산함으로써 얻을 수 있다고 생각할 수 있다.

 

따라서 circulation density를 유도했을 때와 마찬가지로 각 모서리에 대해서 값을 계산하자. 아래 모서리에 대한 flux는 다음과 같다: $$\int_{\text{bottom}} \mathbf{F} \cdot \mathbf{n} ds = - \int_x^{x + \Delta x} N(x', y) dx' - N(x, y) \Delta x$$ 같은 논리를 적용해서 각 모서리에 대해서 계산하면 다음과 같다: $$\begin{align} &\text{bottom}: \quad -N(x, y) \Delta x \\ &\text{top}: \quad N(x, y + \Delta y) \Delta x \\ &\text{left}: \quad -M(x, y) \Delta y \\ &\text{right}: \quad M(x + \Delta x, y) \Delta y \end{align}$$

이제 위에서 구한 값들을 같은 축의 값끼리 더해주면 다음과 같다: $$\begin{align} &\text{bottom and top}: \quad (N(x, y + \Delta y) - N(x, y)) \Delta x \approx \left( \frac{\partial N}{\partial y} \Delta y \right) \Delta x \\ &\text{left and right}: \quad (M(x + \Delta x, y) - M(x, y)) \Delta y \approx \left( \frac{\partial M}{\partial x} \Delta x \right) \Delta y \end{align}$$ 마찬가지로 $\Delta x, \Delta y \to 0$을 상정하므로 위와 같은 근사가 성립한다. 따라서 이 값들을 모두 더해주면 최종적으로 $A$에서의 flux가 되고, 그 값은 $$\left( \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} \right) \Delta x \Delta y$$ 이다. 

우리는 점 $(x, y)$에서 유체가 얼마나 유출 혹은 유입되고 있는지를 측정해야 하므로 위에서 구한 값에 region $A$의 넓이 $\Delta x \Delta y$를 나눠주면 그 값은 $$\frac{\partial M}{\partial x} + \frac{\partial N}{\partial y}$$ 이고, 이 값을 flux density, 혹은 divergence라고 부른다.

Definition 2. The divergence (flux density) of a vector field $\mathbf{F}(x, y) = \langle M(x, y), N(x, y) \rangle$ at the point $(x, y)$ is $$\nabla \cdot \mathbf{F} = \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y}.$$

유도과정에서 알 수 있었듯이, $\mathbf{F}$가 유출되고 있으면 divergence의 값은 양수이고, 유입되고 있으면 음수이다. 따라서 divergence의 부호를 통해 유출되고 있는지, 유입되고 있는지의 여부를 판단할 수 있다. 일반적으로 $\mathbf{F}$가 3차원의 경우, 즉 $\mathbf{F} = \langle M, N, P \rangle$일 때도 $$\nabla \cdot \mathbf{F} = \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} + \frac{\partial P}{\partial z}$$ 와 같이 동일하게 정의한다.

Theorem 1

Theorem 1. If $\mathbf{F} = \langle M, N, P \rangle$ is a vector field with continuous second partial derivatives, then $$\nabla \cdot (\nabla \times \mathbf{F}) = 0.$$

Proof. $$\nabla \cdot (\nabla \times \mathbf{F}) = \frac{\partial}{\partial x} \left( \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z} \right) + \frac{\partial}{\partial y} \left( \frac{\partial M}{\partial z} - \frac{\partial P}{\partial x} \right) + \frac{\partial}{\partial z} \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) \\ = \frac{\partial^2 P}{\partial x \partial y} - \frac{\partial^2 N}{\partial x \partial z} + \frac{\partial^2 M}{\partial y \partial z} - \frac{\partial^2 P}{\partial y \partial x} + \frac{\partial^2 N}{\partial z \partial x} - \frac{\partial^2 M}{\partial z \partial y} = 0. \blacksquare$$

즉 curl의 divergence는 0이다. 만약 어떤 벡터장 $G$가 $G = \nabla \times \mathbf{F}$로 표현된다면 $\nabla \cdot G = 0$이다. 거꾸로 말하면 $\nabla \cdot G \neq 0$이라면 $G$는 어떤 벡터장의 curl로 표현되지 않는다는 뜻이다.