Parametrization of Surfaces

Parametrization of Surfaces

Definition 1. Suppose $\mathbf{r}(u, v) = \langle f(u, v), g(u, v), h(u, v) \rangle$ is a continuous vector function that is defined on a region $R$ in the $uv$-plane and one-to-one on the interior of $R$. We call the range of $\mathbf{r}$ the surface $S$ defined or traced by $\mathbf{r}$. The vector function together with the domain $R$ constitutes a parametrization of the surface. 

곡선의 parametrization과 같은 방법으로 surface의 parametrization을 정의할 수 있다. 2차원이므로 변수는 두 개가 된다.

Definition 2. A parametrized surface $\mathbf{r}(u, v) = \langle f(u, v), g(u, v), h(u, v) \rangle$ is smooth if $\mathbf{r}_u$ and $\mathbf{r}_v$ are continuous and $\mathbf{r}_u \times \mathbf{r}_v$ is never zero on the interior of the parameter domain. 

$\mathbf{r}_u \times \mathbf{r}_v \neq 0$이라는 조건은 영벡터가 아닌 $\mathbf{r}_u$와 $\mathbf{r}_v$가 평행하지 않다는 조건과 동치이다. 따라서 $\mathbf{r}_u \times \mathbf{r}_v$은 항상 오른손 규칙에 따라 두 벡터 모두에 수직한 벡터를 의미한다. 

Area of Parametric Surfaces

다음 그림과 같이 $uv$ 평면에서 작은 직사각형 조각인 $\Delta A_{uv}$를 고려하자. $\mathbf{r}(u, v)$에 의해 $\Delta A_{uv}$의 각 side는 좌표 공간에서 각각 curve들로 변환되고, $\Delta A_{uv}$는 이 curve들로 둘러싸인 'curved patch element' $\Delta \sigma_{uv}$로 변환된다. 

Thomas Calculus 13e 983p.

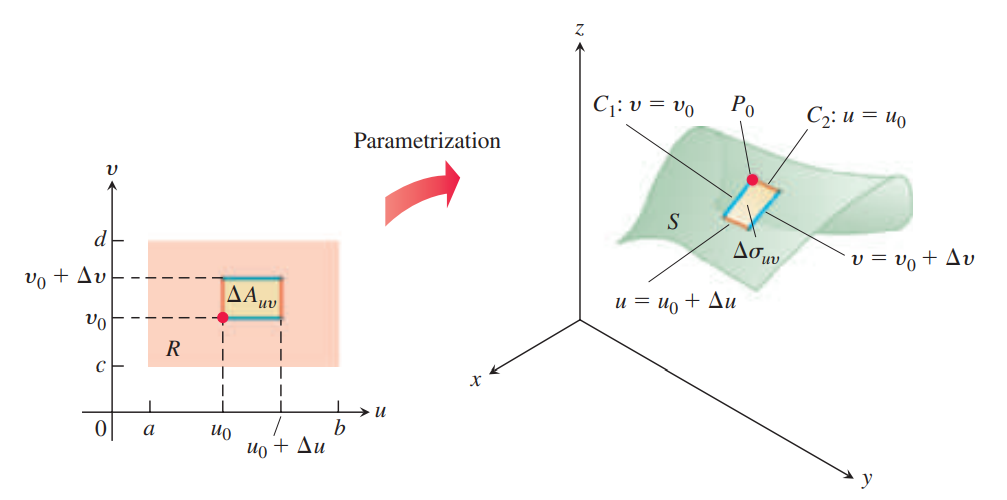
$\Delta \sigma_{uv}$를 확대하면 다음과 같다. $P_0$에서 곡선 $C_1$과 $C_2$의 방향을 가지는 partial derivative는 각각 $\mathbf{r}_u$와 $\mathbf{r}_v$이다. 

Thomas Calculus 13e 983p.

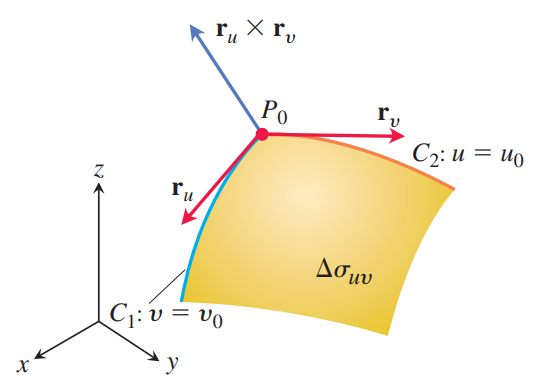
우리가 다루는 surface는 smooth하므로 $\mathbf{r}_u \times \mathbf{r}_v$는 영벡터가 아니고 $P_0$에서 $S$의 tangent plane이다. 이 tangent plane의 넓이는 cross product의 성질에 의해 $| \Delta u \mathbf{r}_u \times \Delta v \mathbf{r}_v | = | \mathbf{r}_u \times \mathbf{r}_v | \Delta u \Delta v$이다.

 

이제 $R$을 잘게 쪼갠 뒤 각 piece에 대해 같은 과정을 반복하고 얻은 tangent plane의 넓이들을 모두 더해준뒤 $\Delta u, \Delta v \to 0$인 극한을 취하자. 이때 값이 수렴하면 적분으로 다룰 수 있고, 이를 다음과 같이 정의한다.

Definition 3. The area of the smooth surface $$\mathbf{r}(u, v) = \langle f(u, v), g(u, v), h(u, v) \rangle, \quad a \leq u \leq b, c \leq v \leq d$$ is $$A = \iint_R | \mathbf{r}_u \times \mathbf{r}_v | dA = \int_c^d \int_a^b | \mathbf{r}_u \times \mathbf{r}_v | du dv.$$

Implicit Surface

곡면이 explict하게 어느 한 변수에 대하여 표현되는 경우가 아닌 implicit한 경우 넓이를 구해보자. 이 경우는 $F(x, y, z) = c$와 같이 $F$의 level curve로 표현된다고 가정할 수 있는데, 이때는 parametrization $\mathbf{r}(u, v)$를 찾기가 힘들다. 따라서 다른 방법으로 differential $d \sigma$를 찾아야 한다.

Thomas Calculus 13e 986p.

 

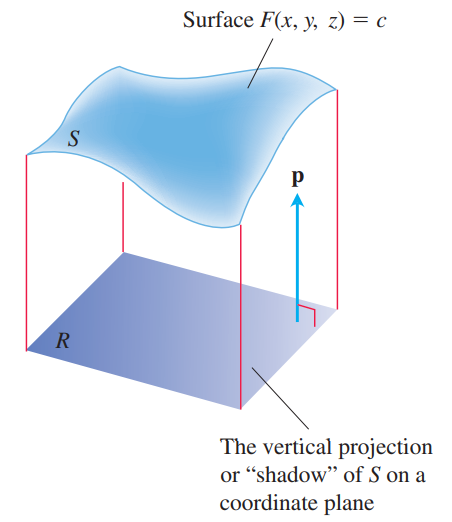
다음 그림과 같이 곡면 $S$를 $xy$ 평면에 projection 시킨 영역 $R$을 고려하자. $S$를 향하는 $R$의 normal vector를 $\mathbf{p}$라고 하자. 이 경우 $\mathbf{p} = \mathbf{k}$이다. $S$는 smooth하므로 $\nabla F$는 0이 아니며 연속이다. 따라서 $\nabla F \cdot \mathbf{p} = \partial_z F$이다. 이때 Implict Function Theorem에 의해 $\frac{dz}{dx} = \frac{\partial_x F}{\partial_z F}$와 $\frac{dz}{dy} = \frac{\partial _y F}{\partial_z F}$를 모두 알 수 있으므로 $F(x, y, z) = c$를 적어도 $z = h(x, y)$와 같은 형식으로 작성할 수 있다. 

 

이제 parameter $u, v$를 $u = x, v = y$와 같이 설정하면 surface $S$는 $$\mathbf{r}(u, v) = \langle u, v, h(u, v) \rangle$$ 과 같이 parametrization될 수 있다. 따라서 $$\mathbf{r}_u = \langle 1, 0, \frac{\partial h}{\partial u} \rangle = \langle 1, 0, - \frac{\partial_x F}{\partial_z F} \rangle \quad \text{  } \quad \mathbf{r}_v = \langle 0, 1, \frac{\partial h}{\partial v} \rangle = \langle 0, 1, - \frac{\partial_y F}{\partial_z F} \rangle$$ 이다. 

 

따라서 $$\mathbf{r}_u \times \mathbf{r}_v = \langle \frac{\partial_x F}{\partial_z F}, \frac{\partial_y F}{\partial_z F}, 1 \rangle = \frac{1}{\partial_z F} \langle \partial_x F, \partial_y, \partial_z F \rangle = \frac{\nabla F}{\partial_z F} \\ = \frac{\nabla F}{\nabla F \cdot \mathbf{p}}$$ 이다. 그러므로 $$d \sigma = |\mathbf{r}_u \times \mathbf{r}_v| du dv = \frac{|\nabla F|}{|\nabla F \cdot \mathbf{p}|} dx dy$$ 이다. 동일한 유도 과정을 $\mathbf{p} = \mathbf{i}, \mathbf{j}$의 경우에도 할 수 있고, 모두 위와 같은 동일한 결과가 나온다. 따라서 우리는 implicit surface의 경우 다음과 같이 넓이를 구할 수 있다.

The area of the surface $F(x, y, z) = c$ over a closed and bounded plane region $R$ is $$\iint_R \frac{|\nabla F|}{|\nabla F \cdot \mathbf{p}|} dA,$$ where $\mathbf{p} = \mathbf{i}, \mathbf{j},$ and $\mathbf{k}$ is normal to $R$ and $\nabla F \cdot \mathbf{p} \neq 0$.

위를 적용하여 $z =f(x, y)$로 표현되는 surface의 area를 찾을 수 있다. $F(x, y, z) = f(x, y) - z = 0$으로 표현될 수 있으므로, 영역 $R$이 $xy$ 평면 위에 있다고 가정하면 $|\nabla F| = \sqrt{(\partial_x f)^2 + (\partial_f f)^2 + 1}$이고 $|\nabla F \cdot \mathbf{p}| = 1$이므로 area는 $$\iint_R \sqrt{(\partial_x f)^2 + (\partial_f f)^2 + 1} dx dy$$ 이다.