동시성의 상대성에 이어서 특수상대성이론의 대표적인 결과인 '시간 팽창'(Time Dilation)과 '길이 수축'(Length Contraction)을 다뤄보자.
11. 시간 팽창 (Time Dilation)

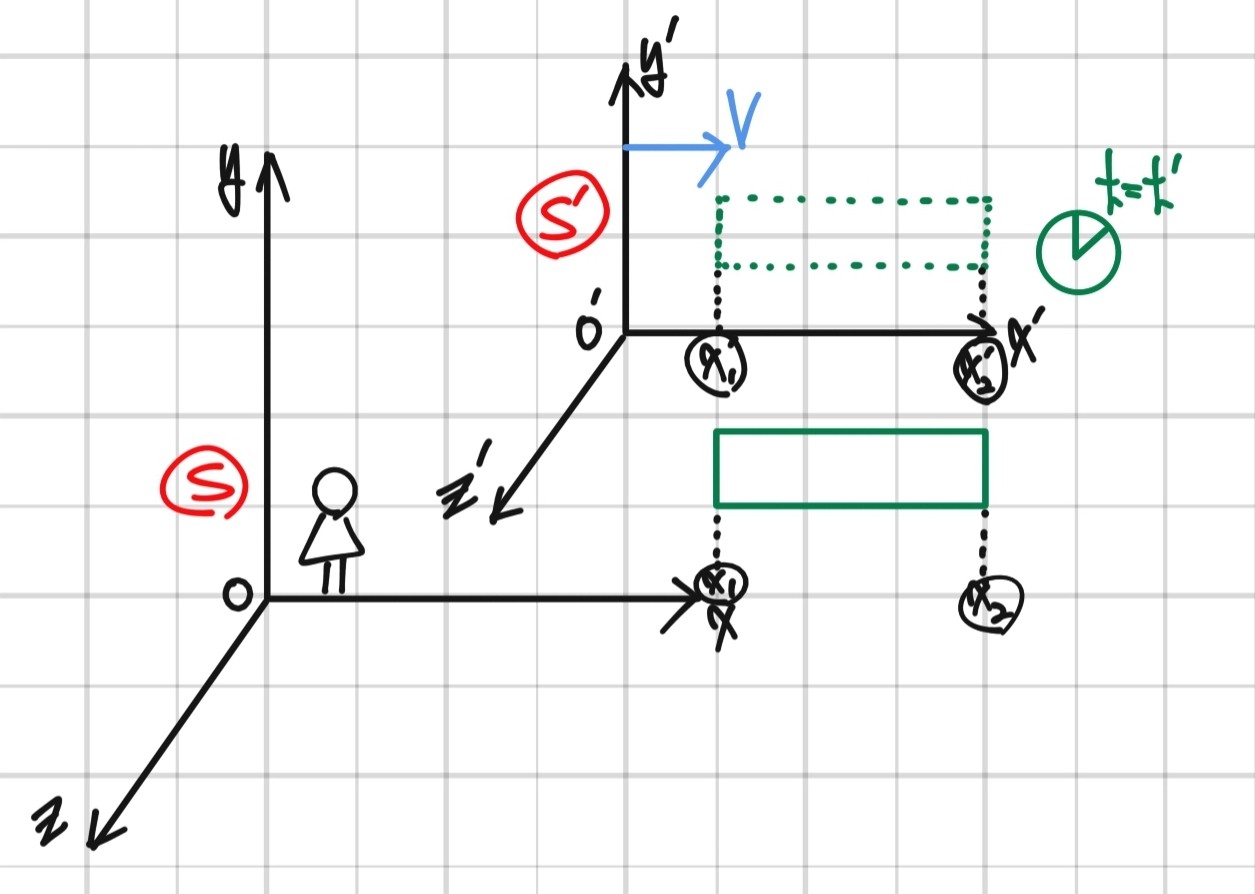
다음 그림과 같이 $S$ 좌표계에 있는 관찰자가 $S$와 $S'$에 있는 시계가 가리키는 시간을 읽는 상황을 고려하자. 시계는 $S$를 기준으로 $x$의 위치에 있다. 이때 관찰자에 대해 정지해 있는 좌표계에서 읽는 시간을 '고유시간'(Proper Time)1이라고 부른다. 위 그림에서 고유시간은 $S$에 있는 관찰자가 읽는 시간이므로 $t = t_1, t = t_2$가 고유시간이다. $S$에서 읽는 고유시간 간격 $t_0$는 $t_0 = t_2 - t_1$이다. 따라서 $S$에 있는 관찰자가 읽어내는 $S'$에 있는 시계가 가리키는 시간 $t = t'_1$과 $t = t'_2$는 로렌츠 변환에 의해
$$t'_1 = \gamma (t_1 - \frac{V \cdot x}{c^2}) \\ t'_2 = \gamma (t_2 - \frac{V \cdot x}{c^2})$$이므로 $S$에서 읽는 $S'$에 있는 두 시계가 가리키는 시각의 간격은 다음과 같다.
$$\Delta t = t'_2 - t'_1 = \gamma (t_2 - \frac{V \cdot x}{c^2}) - \gamma (t_1 - \frac{V \cdot x}{c^2}) = \gamma (t_2 - t_1) = \gamma t_0 \\ \text{Thus,} \,\, \gamma t_0 > t_0 (\because \gamma > 1)$$ 따라서 시간 간격이 늘어나므로 이를 '시간 팽창'이라고 부른다.

이번에는 관찰자가 $S'$에 있어서 각 좌표계에 있는 시계가 가리키는 시간을 읽는 상황을 고려하자. 마찬가지로 S'에서 읽는 고유시간 간격은 $t'_0 = t'_2 - t'_1$이다. 역로렌츠 변환에 의해 $S'$에 읽는 $S$에 있는 시계가 가리키는 시각의 간격을 계산하면 다음과 같다.
$$t_1 = \gamma (t'_1 + \frac{V \cdot x'}{c^2}) \\ t_2 = \gamma (t'_2 + \frac{V \cdot x'}{c^2}) \\ \Delta t = t_2 - t_1 = \gamma (t'_2 + \frac{V \cdot x'}{c^2}) - \gamma (t'_1 + \frac{V \cdot x'}{c^2}) = \gamma (t'_2 - t'_1) = \gamma t'_0 \\ \text{Thus,} \,\, \gamma t'_0 > t'_0 (\because \gamma > 1)$$
로렌츠 변환에서도 언급했듯이, $S$와 $S'$ 각각의 좌표계에서 계산한 시간 팽창은 동일한 정도로 나타난다. 즉 어느 변환으로 계산해도 동일한 결과를 가져오며, 겉으로 나타나는 변수의 모습만 다를 뿐이지 함축된 의미는 둘 다 동일하다.
위의 논의의 결과를 정리하면, 관찰자에 대해서 움직이는 좌표계에 있는 시계는 천천히 간다. 즉 등속도로 상대적으로 움직이는 두 좌표계에 대하여 시간은 항상 관측자가 없는 곳에서 느리게 흐른다. 만약 좌표계의 속력 $V$가 광속 $c$라면 로렌츠 인자는 무한대로 발산하여 시간 간격 또한 무한대로 발산한다. 이는 자명하게 모순이므로 좌표계, 혹은 물체는 빛보다 빠른 속력으로 움직일 수 없다.
12. 길이 수축 (Length Contraction)

이번에는 길이 수축을 살펴보자. 마찬가지로 $S'$의 관찰자가 $S$와 $S'$에 있는 자의 길이를 재는 상황을 고려하자. $S'$에 있는 자는 양끝점이 $x'_1, x'_2$의 위치를 가지고 있고 $S$의 자는 마찬가지로 양끝점이 $x_1, x_2$의 위치를 가지고 있다. $S$에 있는 자의 길이를 재기 위해서는 로렌츠 변환에 의해 $S$의 시간을 알아야 하므로 $S$에는 시계가 놓여 있어 시간이 고정되어야 한다. 이때 관찰자에 대해 정지한 좌표계에서 읽는 길이를 '고유길이'(Proper Length)라고 부르며, $S'$의 관찰자에 대한 고유길이 $L'_0$는 $L'_0 = x'_2 - x'_1$이다. 이때 $x'_2$와 $x'_1$은 S의 정보를 통한 로렌츠 변환에 의해 각각
$$x'_1 = \gamma (x_1 - V \cdot t) \\ x'_2 = \gamma (x_2 - V \cdot t)$$이므로 $S'$ 관찰자에 대하여 움직이는 자의 길이 $L$은 다음과 같다.
$$L'_0 = x'_2 - x'_1 = \gamma (x_2 - V \cdot t) - \gamma (x_1 - V \cdot t) = \gamma (x_2 - x_1) \\ L := x_2 - x_1 = \frac{L'_0}{\gamma} \\ \text{Thus,} \,\, L = \frac{L'_0}{\gamma} < L'_0 (\because \gamma > 1)$$
즉 관찰자에 대해서 움직이는 자의 길이 $L$은 고유길이 $L'_0$보다 항상 작다. 따라서 자의 길이가 줄어드므로 이를 '길이 수축'이라고 부른다.
$S$의 관찰자가 $S$와 $S'$에 있는 자의 길이를 재는 상황을 고려하자. 마찬가지로 자는 $S$에 있는 자는 양끝점이 $x_1, x_2$의 위치를 가지고 있고 $S'$의 자는 양끝점이 $x'_1, x'_2$의 위치를 가지고 있다. 시계는 $S'$에 있어서. 이 시계를 읽음으로써 $S'$의 자의 길이를 잴 수 있다. $S$의 관찰자에 대한 고유길이 $L_0$는 $L_0 = x_2 - x_1$이다. 이때 $x_1$과 $x_2$는 로렌츠 변환에 의해
$$x_1 = \gamma (x'_1 + V \cdot t') \\ x_2 = \gamma (x'_2 + V \cdot t')$$이다. 따라서 $S$의 관찰자가 읽는 $S'$의 자의 길이 $L'$은
$$L_0 = x_2 - x_1 = \gamma (x'_2 + V \cdot t') - \gamma (x'_1 + V \cdot t') = \gamma (x'_2 - x'_1) \\ L' := x'_2 - x'_1 = \frac{L_0}{\gamma} \\ \text{Thus,} \,\, L' = \frac{L_0}{\gamma} < L'0 (\because \gamma > 1)$$의 관계가 성립한다. 즉 관찰자에 대해서 움직이는 자의 길이 $L'$은 고유길이 $L_0$보다 항상 작다.
시간 팽창에서와 마찬가지로 로렌츠 변환과 역로렌츠 변환 중 어느 것을 써도 관찰자에 대해서 움직이는 좌표계에 있는 공간은 줄어든다는 결론을 얻는다. 주의할 것은 이때 줄어드는 방향은 오직 운동방향으로만 움직인다. 로렌츠 변환은 운동방향으로만 변환이 일어나므로, 길이 수축은 운동방향으로만 일어난다.
정리하면, 등속도로 상대적으로 움직이는 두 좌표계에 대하여 공간은 항상 관측자가 없는 곳에서 더 짧아진다. 만약 좌표계의 속력 $V$가 광속 $c$라면 로렌츠 인자는 무한대로 발산하여 자의 길이는 0으로 수렴하게 된다. 이는 물체가 사라진다는 말과 같으므로, 좌표계, 혹은 물체는 빛보다 빠른 속력으로 움직일 수 없다.
유념할 것은, 위의 상황에서는 시간이 팽창하고 공간이 수축한다는 사실을 '확인', 혹은 '검출'하기 위해 불가피하게 그 도구로 시계와 자를 사용했지만, 이것을 단순히 시계가 천천히 가고, 자가 줄어든다는 의미로만 받아들이면 안된다. 예컨대 평면에 +전하가 놓여 있을 때 임의의 위치에 단위전하를 놓았을 때 전하는 전기장의 크기에 비례하는 힘을 받게 된다. 이때 전하를 없애면 그 위치에 전기장이 작용하는 힘은 없어지는가? 그렇지 않다. 단지 전하는 전기장의 존재를 확인 및 검출하는 역할일 뿐이며, 전기장은 모든 공간에 영향력을 행사한다.
시간 팽창, 길이 수축 또한 마찬가지다. 시계와 자는 단지 시간과 공간이 관측자에 따라 변한다는 사실을 확인시켜주는 장치일 뿐이며, 우리는 시간 그 자체, 공간 그 자체가 팽창하고 수축하는 것으로 받아들여야 한다.
- 로렌츠는 고유시간을 '보편적 시간'(Universal Time)이라고 불렀다. [본문으로]