Directional derivative를 도입하여 미분의 방향을 굳이 $x, y$축으로 한정할 필요가 없었듯이, 적분 또한 $x, y, z$에 대해서만이 아니라 일반적인 곡선 위에서 정의할 수 있다.
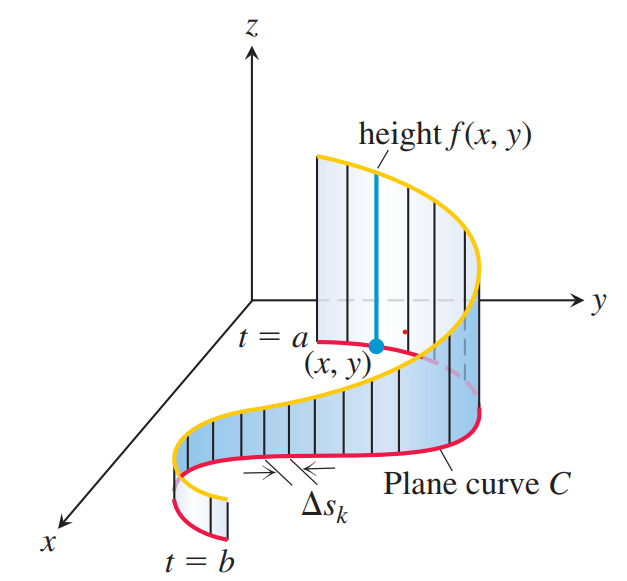
함수 $f(x, y)$가 $\mathbb{r}(t) = \langle x(t), y(t) \rangle (a \leq t \leq b)$ 위에서 정의된다고 하자. 늘 그래왔던 것처럼 $C$를 $n$조각으로 짤라 partition을 구성하고, 각 piece의 길이를 $\Delta s_k$라 하자. 각 piece에서 임의로 point들을 추출하여 Riemann sum을 구성하면 $$\sum_{k=1}^n f(x_k, y_k) \Delta s_k$$이고, $n$의 크기를 무한히 증가시킬 때 partition의 norm이 0으로 수렴하여 극한이 하나의 값으로 수렴할 때 그 값을 아래 정의와 같이 $C$ 위에서 $f$의 line integral, 선적분이라고 한다.
Line Integral of a Scalar Function
Definition 1. If $f$ is defined on a curve $C$ given parametrically by $\mathbb{r}(t) = \langle x(t), g(t), h(t) \rangle, a \leq t \leq b,$ then the line integral of $f$ over $C$ is $$\int_C f(x, y, z) ds = \lim_{n \to \infty} \sum_{k=1}^n f(x_k, y_k, z_k) \Delta s_k,$$ provided this limit exists.
$ds$는 arc length parameter이므로 $$ds = |\mathbb{v}(t)| dt$$를 만족한다. 따라서 위 line integral은 실제로 곡선 $C$의 parametrization $\mathbb{r}(t) = \langle x(t), y(t), z(t) \rangle, (a \leq t \leq b)$에 의해 다음과 같이 계산될 수 있다. $$\int_C f(x, y, z) ds = \int_a^b f(x(t), y(t), z(t)) |\mathbb{v}(t)| dt$$ 당연하게도, $C$에 대해 어떤 parametrization을 가지고 smooth하면 오든 적분의 값은 변하지 않는다.
Additivity
Piecewise smooth curve $C$가 있다고 하자. 이때 $C$를 적당히 $n$개의 curve $C_1, ..., C_n$으로 분할하면 $$\int_C f ds = \int_{C_1} f ds + \cdots + \int_{C_n} f ds$$가 성립한다.
Line Integral of a Vector Field
Definition 2. Let $\mathbf{F}$ be a vector field with continuous components defined along a smooth curve $C$ parametrized by $\mathbb{r}(t), a \leq t \leq b$. Then the line integral of $\mathbf{F}$ along $C$ is $$\int_C \mathbf{F} \cdot \mathbf{T} ds = \int_C \mathbf{F} \cdot d\mathbb{r}.$$
$\mathbf{T}$는 unit tangent vector이다. $\mathbf{T} = \frac{\mathbf{v}}{|\mathbf{v}|} = \frac{1}{|\mathbf{v}|} \cdot \frac{d \mathbf{r}}{dt}$이고 $ds = |\mathbf{v}| dt$이므로 위 정의에서 등식이 성립한다. Scalar function과는 다르게 vector field는 vector를 내놓으므로 주어진 곡선 $C$에 대해서 적분할 때 $C$의 진행 방향의 tangential component만을 취하여 적분해준다. 구체적인 계산은 곡선 $C$를 smooth하게 parametrize하여 $t$에 대해 적분하며, $d \mathbf{r} = \mathbf{v} dt$이므로 $$\int_{C} \mathbf{F} \cdot d \mathbb{r} = \int_a^b \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{v}(t) dt$$이다.
직관적으로 이해해보자. 곡선 $C$가 $\mathbf{r}(t) = \langle x(t), y(t), z(t) \rangle$으로 paramatrize된다고 하자. 이때 $d \mathbf{r} = \mathbf{v} dt$이기도 하지만, $dx = x'(t) dt, dy = y'(t) dt, dz = z'(t) dt$이므로 $d \mathbf{r} = \langle dx, dy, dz \rangle$라고도 쓸 수 있다. $\mathbf{F}(x, y, z) = \langle f(x, y, z), g(x, y, z), h(x, y, z) \rangle$라고 하면 다음이 성립한다. $$\int_C \mathbf{F} \cdot d \mathbf{r} = \int_C f dx + g dy + h dz = \int_C dF$$ Vector field $\mathbf{F}$의 경우 주어진 curve $C$에 대해서 적분하려면 우선 $C$의 tangential 성분만을 취해야 하고, 그렇게 취해진 $\mathbf{F}$를 $F$라고 하자. 그러므로 Vector field의 line integral이란 결국 주어진 곡선 $C$를 따라 취해진 $F$를 $C$에 대하여 전부 더해주라는 뜻이다.