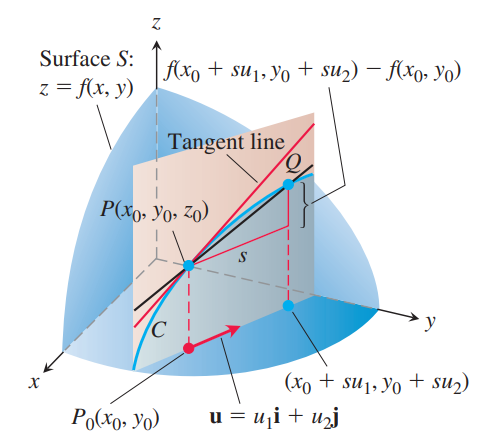
Double IntegralTwo-variable function의 definite ingetral을 다뤄보자. Single variable에서 정의한 definite integral과 별반 다를 건 없다. 다만 변수가 두 개가 되었으므로 partition이라든지, norm이라든지 하는 대상을 조금 확장하여서 정의하고 이를 기반으로 Riemann sum과 그 극한으로 double integral을 정의한다. 함수 $z = f(x, y)$가 있다. 일변수에서는 interval을 잘게 쪼갰다면, 이제는 rectangular region을 $x, y$축으로 잘게 쪼갠다. 이렇게 잘게 쪼갠 piece들은 어떻게든 numbering하여 모은 집합을 partition $P$이라고 하고, 이 piece들의 가로, 세..

Introduction 다변수함수의 극값을 찾기 위한 방법 중 하나로 second derivative test가 있었다. 그런데 만약 함수의 domain이 명시적으로 주어진 것이 아닌, 예컨대 어떤 방정식 $g(x, y, z) = 0$으로 표현되는 "구속조건(constraint)"으로 주어진다면 test를 적용하기가 쉽지 않다. 물론 어찌어찌 parametrize하여 명시적으로 구할 수도 있겠지만, 대게 쉽지 않다. 때문에 구속조건 자체를 활용하여 극값을 구하는 방법이 필요한데 그 결과가 바로 Lagrange multiplier, 라그랑주 승수법이다. 2차원으로 한정지어서 생각해보자. 다음 그림과 같이 구속조건 $g(x, y) = c$ ($h(x, y) = g(x, y) - c$ $= 0$으로도 정의할 ..

Local Maximum and MinimumDefinition 1. Let $f(x, y)$ be defined on a region $R$ containing the point $(a, b)$. Then 1. $f(a, b)$ is a local maximum value of $f$ if $f(a, b) \geq f(x, y)$ for all domain points $(x, y)$ in an open disk centered at $(a, b)$. 2. $f(a, b)$ is a local minimum value of $f$ if $f(a, b) \leq f(x, y)$ for all domain points $(x, y)$ in an open disk centered at $(a, b)$. Si..

Tangent PlaneDefinition 1. The tangent plane to the level surface $f(x, y, z) = c$ of a differentiable function $f$ at a point $P_0$ where the gradient is not zero is the plane through $P_0$ normal to $\nabla f |_{P_0}$. The normal line of the surface at $P_0$ is the line through $P_0$ parallel to $\nabla f |_{P_0}$. 위와 같이 정의되는 tangent plane, 즉 접평면은 정의에 따라 다음과 같이 계산되고, normal line도 마찬가지다. $$\nab..

Directional DerivativeDefinition 1. The derivative of $f$ at $P_0 (x_0, y_0)$ in the direction of the unit vector $\mathbb{u} = u_1 \mathbb{i} + u_2 \mathbb{j}$ is the number $$\left( \frac{df}{ds} \right)_{\mathbb{u}, P_0} = \lim_{s \to 0} \frac{f(x_0 + su_1, y_0 + su_2) - f(x_0, y_0)}{s},$$ provided the limit exists. It is also denoted by $$D_{\mathbb{u}}f(P_0) \text{  or  } D_{\mathbb{u}}f \b..

Theorem 1Theorem 1. Suppose that $F(x, y)$ is differentiable and that the equation $F(x, y) = 0$ defines $y$ as a differentiable function of $x$. Then at any point where $\partial_y F \neq 0,$ $$\frac{dy}{dx} = - \frac{\partial_x F}{\partial_y F}.$$Proof. Since $F(x, y) = 0$, the derivative $\frac{dF}{dx}$ must be zero. By the Chain Rule, we find $$0 = \frac{dF}{dx} = \frac{\partial F}{\partial ..

Theorem 1Theorem 1. If $w=f(x, y)$ is differentiable and if $x = x(t), y=y(t)$ are differentiable functions of $t$, then the composition $w=f(x(t), y(t))$ is a differentiable function of $t$ and $$\frac{dw}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}.$$Proof. Let $\Delta x, \Delta y$ and $\Delta w$ be the increments that result from changing $t..

Partial DerivativeDefinition 1. The partial derivative of $f(x, y)$ with respect to $x$ at the point $(x_0, y_0)$ is $$\frac{\partial f}{\partial x} \Bigg|_{(x_0, y_0)} = \lim_{h \to 0} \frac{f(x_0 + h, y_0) - f(x_0, y_0)}{h},$$ provided the limit exists. The partial derivative with respect to $y$ is defined in the same way.특정 변수를 상수로 취급하고 한 변수만 다룬다는 의미에서 편미분이라고 말한다. 기호로는 $\frac{\partial f}{\par..

프로그램(Program)은 일종의 명령어 집합이다. 컴퓨터에서 특정 기능을 수행하도록 프로그램을 만들기 위해서는 이 명령어들을 구조와 논리에 맞게 작성해 주어야 한다. 이때 우리는 다양한 프로그래밍 언어를 사용해 코드(code)를 작성하고, 이러한 행위를 코딩(coding)이라고 부른다.     프로그래밍 언어라고 하면 대부분 python, C, C++, Java 등을 떠올릴 것이다. 이와 같은 언어들을 고급 언어(High Level Language)라고 하고, 이와 구분되는 언어로 저급 언어(Low Level Language)가 있다. 고급, 저급과 같은 말의 뉘앙스 때문에 오해할 수도 있지만 두 언어는 단지 사용자 친화적인지, 컴퓨터 친화적인지에 따라 구분된다. 컴퓨터가 더 이해하기 쉬운 언어면 저급..

컴퓨터에서 문자를 처리하려면 당연하게도 컴퓨터가 이해할 수 있는 언어로 (2진수, 8진수, 16진수 등등...) 변환하여야 한다. 그렇다면 각 문자들에 서로 다른 값들을 할당해 주어야 하고, 이를 정리한 문자표가 필요할 것이다. 이처럼 값이 할당되어서 컴퓨터가 이해하고 처리할 수 있는 문자들을 모아놓은 모음을 문자 집합(Character Set)이라고 한다.     문자 집합에 속한 문자를 컴퓨터가 처리할 수 있게 변환하는 과정을 문자 인코딩(Character Encoding), 그 반대의 과정을 문자 디코딩(Character Decoding)이라고 한다. 과거부터 지금까지 다양한 문자 집합과 인코딩, 디코딩 방법이 제안되었고, 그 중 몇 가지를 살펴보도록 하자. 아스키 코드    초창기 컴퓨터는 아스키..